Bài 9.37 trang 60 sách bài tập Toán 8 Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng giải bài toán thực tế liên quan đến ứng dụng của hàm số bậc nhất. Bài tập này đòi hỏi học sinh phải hiểu rõ về cách xác định hàm số, tìm điểm thuộc đồ thị hàm số và giải quyết các bài toán liên quan đến khoảng cách.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 9.37 trang 60 sách bài tập Toán 8 Kết nối tri thức, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Cho tam giác ABC vuông tại đỉnh A. Gọi AD là đường cao của tam giác. Biết rằng \(BD = 2cm,CD = 8cm.\) Hãy tính độ dài các cạnh AB, AC và chiều cao AD của tam giác ABC.
Đề bài
Cho tam giác ABC vuông tại đỉnh A. Gọi AD là đường cao của tam giác. Biết rằng \(BD = 2cm,CD = 8cm.\) Hãy tính độ dài các cạnh AB, AC và chiều cao AD của tam giác ABC.
Phương pháp giải - Xem chi tiết
+ Sử dụng kiến thức về định lý (trường hợp đồng dạng góc – góc) để tính AD: Nếu hai góc của tam giác lần lượt bằng hai góc của tam giác kia thì hai tam giác đó đồng dạng với nhau.
+ Sử dụng kiến thức định lí Pythagore để tính độ dài AB, AC: Trong một tam giác vuông, bình phương cạnh huyền bằng tổng các bình phương của hai cạnh góc vuông.
Lời giải chi tiết
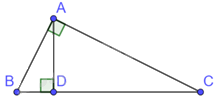
Vì AD là đường cao của tam giác ABC nên \(AD \bot BC\). Do đó, \(\widehat {ADB} = \widehat {ADC} = {90^0}\)
Tam giác ABD và tam giác CAD có:
\(\widehat {ADB} = \widehat {ADC} = {90^0}\left( {cmt} \right),\widehat {BAD} = \widehat C\) (cùng phụ với góc DAC). Do đó, $\Delta ABD\backsim \Delta CAD\left( g-g \right)$
Suy ra: \(\frac{{AD}}{{CD}} = \frac{{BD}}{{AD}}\) nên \(A{D^2} = CD.BD = 2.8 = 16\)
Do đó, \(AD = 4cm\)
Áp dụng định lí Pythagore vào tam giác ABD vuông tại D có:
\(A{B^2} = A{D^2} + B{D^2} = 16 + {2^2} = 20\) nên \(AB = 2\sqrt 5 cm\)
Áp dụng định lí Pythagore vào tam giác ACD vuông tại D có:
\(A{C^2} = A{D^2} + C{D^2} = 16 + {8^2} = 80\) nên \(AC = 4\sqrt 5 cm\)
Bài 9.37 sách bài tập Toán 8 Kết nối tri thức yêu cầu học sinh giải quyết một bài toán thực tế liên quan đến việc xác định vị trí của một điểm trên mặt phẳng tọa độ dựa trên thông tin về khoảng cách đến các trục tọa độ. Để giải bài toán này, học sinh cần nắm vững kiến thức về:
Trước khi đi vào giải bài toán cụ thể, chúng ta cần phân tích đề bài để xác định rõ các yếu tố quan trọng. Trong bài 9.37, đề bài cung cấp thông tin về một điểm A có tọa độ (x; y) và khoảng cách của điểm A đến các trục tọa độ. Nhiệm vụ của học sinh là tìm tọa độ của điểm A dựa trên các thông tin đã cho.
Để giải bài 9.37, chúng ta có thể sử dụng phương pháp sau:
Ví dụ, nếu đề bài cho biết điểm A cách trục Ox một khoảng bằng 3 đơn vị và cách trục Oy một khoảng bằng 4 đơn vị, thì ta có thể suy ra rằng x = 4 và y = 3 (hoặc x = -4 và y = 3, x = 4 và y = -3, x = -4 và y = -3). Tuy nhiên, cần lưu ý rằng không phải lúc nào cũng có thể xác định được tọa độ của điểm A một cách duy nhất. Trong một số trường hợp, có thể có nhiều điểm A thỏa mãn điều kiện của bài toán.
Ngoài bài 9.37, sách bài tập Toán 8 Kết nối tri thức còn có nhiều bài tập tương tự liên quan đến ứng dụng của hàm số bậc nhất. Các bài tập này thường yêu cầu học sinh:
Để giải các bài tập về hàm số bậc nhất một cách hiệu quả, học sinh nên:
Bài 9.37 trang 60 sách bài tập Toán 8 Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng giải bài toán thực tế liên quan đến ứng dụng của hàm số bậc nhất. Hy vọng rằng với lời giải chi tiết và các hướng dẫn trên, các em học sinh sẽ tự tin giải bài tập này và các bài tập tương tự một cách hiệu quả.
| Khái niệm | Giải thích |
|---|---|
| Hàm số bậc nhất | Hàm số có dạng y = ax + b, trong đó a và b là các số thực. |
| Đồ thị hàm số | Tập hợp tất cả các điểm (x; y) thỏa mãn phương trình y = ax + b. |
| Hệ tọa độ | Hệ thống dùng để xác định vị trí của một điểm trên mặt phẳng. |