Bài 9.34 trang 59 sách bài tập Toán 8 Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng giải bài toán thực tế liên quan đến ứng dụng của tam giác đồng dạng. Bài tập này thường yêu cầu học sinh vận dụng kiến thức về tỉ lệ thức, tam giác đồng dạng để tìm ra các đại lượng chưa biết.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 9.34 trang 59, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Cho tam giác ABC vuông cân tại đỉnh A có đường cao AH. Biết rằng (AB = 4cm), hãy tính độ dài cạnh đáy BC và chiều cao AH.
Đề bài
Cho tam giác ABC vuông cân tại đỉnh A có đường cao AH. Biết rằng \(AB = 4cm\), hãy tính độ dài cạnh đáy BC và chiều cao AH.
Phương pháp giải - Xem chi tiết
+ Sử dụng kiến thức định lí Pythagore để tính BC: Trong một tam giác vuông, bình phương cạnh huyền bằng tổng các bình phương của hai cạnh góc vuông.
+ Sử dụng kiến thức tam giác cân để chứng minh được \(AH = \frac{1}{2}BC\)
Lời giải chi tiết
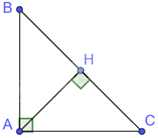
Áp dụng định lý Pythagore vào tam giác ABC vuông tại A ta có:
\(B{C^2} = A{B^2} + A{C^2} = {4^2} + {4^2} = 32\)
Nên \(BC = \sqrt {32} = 4\sqrt 2 \left( {cm} \right)\).
Vì tam giác ABC vuông cân tại A có AH là đường cao nên AH vừa là đường cao vừa là đường trung tuyến của tam giác ABC. Khi đó AH là đường trung tuyến ứng với cạnh huyền trong tam giác vuông ABC.
Do đó: \(AH = HC = HB = \frac{1}{2}BC\)
Suy ra \(AH = \frac{1}{2}BC = 2\sqrt 2 \left( {cm} \right)\)
Bài 9.34 trang 59 sách bài tập Toán 8 Kết nối tri thức yêu cầu chúng ta giải quyết một bài toán thực tế liên quan đến việc tính chiều cao của một ngọn cây dựa vào bóng của nó và bóng của một người. Để giải bài toán này, chúng ta cần hiểu rõ về ứng dụng của tam giác đồng dạng trong việc giải quyết các bài toán thực tế.
Một người có chiều cao 1,6m đứng cách một ngọn cây một khoảng là 10m. Biết bóng của người đó trên mặt đất dài 2m và bóng của ngọn cây dài 20m. Tính chiều cao của ngọn cây.
Bài toán này có thể được giải quyết bằng cách sử dụng tính chất của tam giác đồng dạng. Chúng ta có thể hình dung hai tam giác đồng dạng: tam giác tạo bởi người và bóng của người, và tam giác tạo bởi ngọn cây và bóng của ngọn cây. Tỉ lệ giữa chiều cao của người và chiều dài bóng của người sẽ bằng tỉ lệ giữa chiều cao của cây và chiều dài bóng của cây.
Gọi chiều cao của ngọn cây là h (m).
Ta có tỉ lệ thức sau:
h / 20 = 1.6 / 2
Giải phương trình trên, ta được:
h = (1.6 * 20) / 2
h = 16
Vậy chiều cao của ngọn cây là 16m.
Tại sao chúng ta có thể sử dụng tam giác đồng dạng để giải bài toán này? Bởi vì khi ánh sáng mặt trời chiếu xuống, các góc tạo bởi bóng của người và cây với mặt đất là bằng nhau (góc tạo bởi tia sáng mặt trời và mặt đất). Do đó, hai tam giác được tạo thành là đồng dạng theo trường hợp góc - góc (AA). Khi hai tam giác đồng dạng, các cạnh tương ứng của chúng tỉ lệ với nhau.
Các bài tập tương tự bài 9.34 thường yêu cầu tính chiều cao của các vật thể khác nhau (cột điện, tòa nhà,...) dựa vào bóng của chúng và bóng của một vật thể có chiều cao đã biết. Để giải các bài tập này, bạn cần:
Ứng dụng của tam giác đồng dạng không chỉ giới hạn trong việc tính chiều cao của các vật thể. Nó còn được sử dụng trong nhiều lĩnh vực khác như:
Để củng cố kiến thức về ứng dụng của tam giác đồng dạng, bạn có thể tự giải các bài tập sau:
Bài 9.34 trang 59 sách bài tập Toán 8 Kết nối tri thức là một bài tập quan trọng giúp học sinh hiểu rõ về ứng dụng của tam giác đồng dạng trong việc giải quyết các bài toán thực tế. Bằng cách nắm vững kiến thức và rèn luyện kỹ năng giải bài tập, các em học sinh sẽ tự tin hơn trong việc học môn Toán.
| Đại lượng | Giá trị |
|---|---|
| Chiều cao người | 1.6m |
| Khoảng cách từ người đến cây | 10m |
| Chiều dài bóng người | 2m |
| Chiều dài bóng cây | 20m |
| Chiều cao cây | 16m |