Bài 9.29 trang 57 sách bài tập Toán 8 thuộc chương trình Kết nối tri thức với cuộc sống là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng áp dụng kiến thức về hình học đã học vào giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 9.29, giúp các em học sinh nắm vững phương pháp giải và tự tin hơn trong các bài kiểm tra.
Cho hai điểm M, N lần lượt nằm trên hai cạnh AB, AC của tam giác ABC sao cho \(\widehat {ABN} = \widehat {ACM}.\)
Đề bài
Cho hai điểm M, N lần lượt nằm trên hai cạnh AB, AC của tam giác ABC sao cho \(\widehat {ABN} = \widehat {ACM}.\) Gọi O là giao điểm của BN và CM. Chứng minh rằng:
a) \(AM.AB = AN.AC\)
b) \(OM.OC = ON.OB\)
Phương pháp giải - Xem chi tiết
+ Sử dụng kiến thức về định lý (trường hợp đồng dạng cạnh – góc – cạnh): Nếu hai cạnh của tam giác này tỉ lệ với hai cạnh của tam giác kia và góc tạo bởi các cặp cạnh đó bằng nhau thì hai tam giác đó đồng dạng với nhau.
+ Sử dụng kiến thức về định lý (trường hợp đồng dạng góc – góc): Nếu hai góc của tam giác lần lượt bằng hai góc của tam giác kia thì hai tam giác đó đồng dạng với nhau.
Lời giải chi tiết
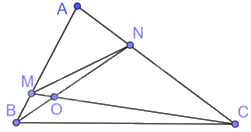
a) Tam giác ABN và tam giác ACM có:
\(\widehat A\;chung,\widehat {ABN} = \widehat {ACM}\left( {gt} \right)\)
Do đó, $\Delta ABN\backsim \Delta ACM\left( g-g \right)$
Suy ra: \(\frac{{AB}}{{AC}} = \frac{{AN}}{{AM}}\) nên \(AM.AB = AN.AC\)
b) Tam giác BOM và tam giác CON có:
\(\widehat {MBO} = \widehat {NCO}\)(gt), \(\widehat {MOB} = \widehat {NOC}\) (hai góc đối đỉnh)
Nên $\Delta BOM\backsim \Delta CON\left( g-g \right)$
Suy ra: \(\frac{{OM}}{{ON}} = \frac{{OB}}{{OC}}\) nên \(OM.OC = ON.OB\)
Bài 9.29 yêu cầu chúng ta xét hình thang ABCD (AB // CD) có hai đường chéo AC và BD cắt nhau tại O. Chúng ta cần chứng minh rằng OA.OD = OB.OC. Đây là một bài toán điển hình về ứng dụng tính chất của tam giác đồng dạng trong hình thang.
Để chứng minh OA.OD = OB.OC, chúng ta cần tìm mối liên hệ giữa các đoạn thẳng này. Nhận thấy rằng hai tam giác AOB và COD có các góc bằng nhau (do AB // CD), chúng ta có thể suy ra hai tam giác này đồng dạng.
Xét tam giác AOB và tam giác COD, ta có:
Vậy, tam giác AOB đồng dạng với tam giác COD theo trường hợp góc - góc - góc (AAA).
Vì tam giác AOB đồng dạng với tam giác COD, ta có tỉ lệ thức:
OA/OC = OB/OD
Suy ra: OA.OD = OB.OC (đpcm)
Bài toán này có thể được mở rộng bằng cách thay đổi vị trí của các điểm hoặc thêm các điều kiện khác. Ví dụ, chúng ta có thể xét trường hợp hình thang cân hoặc hình thang vuông.
Một số bài tập tương tự mà các em có thể tham khảo:
Tỉ lệ thức là một biểu thức thể hiện mối quan hệ giữa hai tỉ số bằng nhau. Trong trường hợp này, tỉ lệ thức OA/OC = OB/OD cho chúng ta biết rằng các đoạn thẳng OA và OC tỉ lệ với các đoạn thẳng OB và OD.
Tam giác đồng dạng là hai tam giác có các góc bằng nhau và các cạnh tương ứng tỉ lệ. Việc chứng minh tam giác đồng dạng là một bước quan trọng trong việc giải quyết nhiều bài toán hình học.
Khi giải bài tập hình học, các em nên:
Bài toán về tam giác đồng dạng và tỉ lệ thức có nhiều ứng dụng trong thực tế, chẳng hạn như:
Bài 9.29 trang 57 Sách bài tập Toán 8 - Kết nối tri thức là một bài toán quan trọng giúp học sinh rèn luyện kỹ năng giải quyết các bài toán hình học. Hy vọng rằng với lời giải chi tiết và dễ hiểu này, các em sẽ tự tin hơn trong việc học tập và làm bài.
Giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán. Chúc các em học tốt!