Bài 7.24 trang 27 sách bài tập Toán 8 Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng giải bài toán thực tế liên quan đến các ứng dụng của tam giác đồng dạng. Giaitoan.edu.vn cung cấp lời giải chi tiết, dễ hiểu, giúp các em nắm vững kiến thức và tự tin giải các bài tập tương tự.
Chúng tôi hiểu rằng việc giải toán đôi khi có thể gặp khó khăn. Vì vậy, đội ngũ giáo viên giàu kinh nghiệm của chúng tôi đã biên soạn lời giải bài 7.24 trang 27 một cách cẩn thận, đảm bảo tính chính xác và dễ tiếp thu.
Đồ thị sau biểu diễn vận tốc xe máy (tính bằng km/h) của anh Nam dưới dạng một hàm số của thời gian t (tính bằng phút)
Đề bài
Đồ thị sau biểu diễn vận tốc xe máy (tính bằng km/h) của anh Nam dưới dạng một hàm số của thời gian t (tính bằng phút)
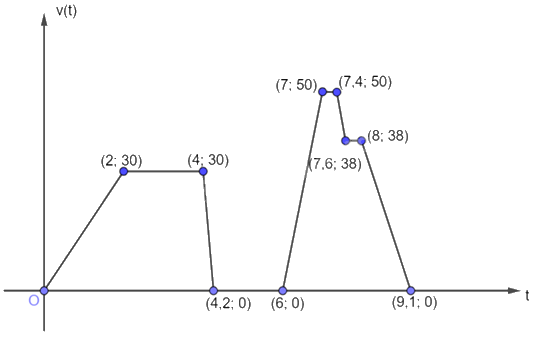
Dựa vào đồ thị trên, hãy trả lời các câu hỏi sau:
a) Anh Nam đi nhanh nhất trong khoảng thời gian nào?
b) Vận tốc của anh Nam bằng 0 trong khoảng thời gian nào?
c) Vận tốc của anh Nam trong khoảng thời gian từ 2 phút đến 4 phút là bao nhiêu?
d) Trong khoảng thời gian nào anh Nam đi với vận tốc 38km/h?
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức nhận biết tọa độ của một điểm trong mặt phẳng tọa độ: Lấy một điểm M bất kì trong mặt phẳng tọa độ Oxy. Từ M kẻ các đường thẳng vuông góc với các trục tọa độ. Giả sử các đường thẳng vuông góc này cắt trục hoành tại điểm \({x_0}\) và cắt trục tung tại điểm \({y_0}.\) Khi đó, cặp số \(\left( {{x_0};{y_0}} \right)\) gọi là tọa độ của điểm M và kí hiệu \(M\left( {{x_0};{y_0}} \right),\) \({x_0}\) được gọi là hoành độ và \({y_0}\) được gọi là tung độ của điểm M.
Lời giải chi tiết
a) Anh Nam đi nhanh nhất trong khoảng thời gian từ 7 phút đến 7,4 phút.
b) Vận tốc của anh Nam bằng 0 trong khoảng thời gian từ 4,2 phút đến 6 phút.
c) Vận tốc của anh Nam trong khoảng thời gian từ 2 phút đến 4 phút là 30km/h.
d) Trong khoảng thời gian từ 7,6 phút đến 8 phút, anh Nam đi với vận tốc 38km/h.
Bài 7.24 trang 27 sách bài tập Toán 8 Kết nối tri thức yêu cầu học sinh vận dụng kiến thức về tam giác đồng dạng để giải quyết một bài toán thực tế. Bài toán thường liên quan đến việc tính chiều cao của một vật thể dựa trên bóng của nó và góc tạo bởi tia nắng mặt trời.
Thông thường, bài toán sẽ cung cấp các thông tin về chiều cao của một vật thể, chiều dài bóng của vật thể đó, và góc tạo bởi tia nắng mặt trời với mặt đất. Học sinh cần sử dụng các tỉ lệ thức trong tam giác đồng dạng để tính toán các đại lượng chưa biết.
Để giải bài 7.24 trang 27, học sinh cần thực hiện các bước sau:
Giả sử, một cột điện cao 6m có bóng dài 8m trên mặt đất. Góc tạo bởi tia nắng mặt trời với mặt đất là 30 độ. Hãy tính chiều cao của một người đứng gần cột điện, biết rằng bóng của người đó dài 2m.
Giải:
Gọi chiều cao của người đó là h. Ta có hai tam giác đồng dạng: tam giác tạo bởi cột điện và bóng của nó, và tam giác tạo bởi người đó và bóng của người đó.
Áp dụng tỉ lệ thức, ta có:
h / 2 = 6 / 8
=> h = (6 * 2) / 8 = 1.5m
Vậy, chiều cao của người đó là 1.5m.
Kiến thức về tam giác đồng dạng có ứng dụng rộng rãi trong thực tế, chẳng hạn như:
Để rèn luyện thêm kỹ năng giải bài toán về tam giác đồng dạng, bạn có thể tham khảo các bài tập tương tự trong sách bài tập Toán 8 Kết nối tri thức hoặc trên các trang web học toán online.
Bài 7.24 trang 27 sách bài tập Toán 8 Kết nối tri thức là một bài tập thú vị và hữu ích, giúp học sinh củng cố kiến thức về tam giác đồng dạng và rèn luyện kỹ năng giải bài toán thực tế. Hy vọng rằng, với hướng dẫn chi tiết này, các em sẽ tự tin giải bài tập và đạt kết quả tốt trong môn Toán.