Bài 3.23 trang 42 sách bài tập Toán 8 Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng giải bài toán thực tế liên quan đến các ứng dụng của hàm số bậc nhất. Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Chúng tôi luôn cố gắng cung cấp nội dung chính xác, đầy đủ và dễ tiếp thu, hỗ trợ tối đa cho quá trình học tập của các em.
Chứng minh hình bình hành có hai đường cao xuất phát từ một đỉnh bằng nhau là một hình thoi.
Đề bài
Chứng minh hình bình hành có hai đường cao xuất phát từ một đỉnh bằng nhau là một hình thoi.
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức về dấu hiệu nhận biết hình thoi để chứng minh: Hình bình hành có một đường chéo là đường phân giác của một góc là hình thoi.
Lời giải chi tiết
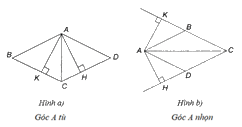
Xét hình bình hành ABCD có đường cao AH (H thuộc đường thẳng CD), và đường cao AK (K thuộc đường thẳng BC) thỏa mãn \(AH = AK\)
Tam giác ACH và tam giác ACK có:
\(\widehat {AHC} = \widehat {AKC} = {90^0}\), \(AH = AK\), cạnh AC chung
Do đó, \(\Delta ACH = \Delta ACK\) (ch – cgv)
Suy ra: \(\widehat {ACK} = \widehat {ACH}\) nên CA là tia phân giác góc BCD.
Hình bình hành ABCD có CA là tia phân giác góc BCD nên ABCD là hình thoi.
Bài 3.23 trang 42 sách bài tập Toán 8 Kết nối tri thức yêu cầu học sinh vận dụng kiến thức về hàm số bậc nhất để giải quyết một bài toán thực tế. Bài toán thường liên quan đến việc xác định hàm số biểu diễn mối quan hệ giữa hai đại lượng, tính giá trị của hàm số tại một điểm cho trước, hoặc tìm điều kiện để hàm số thỏa mãn một tính chất nào đó.
Trước khi bắt đầu giải bài, điều quan trọng là phải đọc kỹ đề bài, hiểu rõ các thông tin đã cho và xác định chính xác yêu cầu của bài toán. Cần chú ý đến các đơn vị đo lường, các điều kiện ràng buộc và các giả thiết được đưa ra trong đề bài.
Hàm số bậc nhất có dạng y = ax + b, trong đó a và b là các hằng số. Để giải bài toán, cần xác định được các giá trị của a và b dựa trên các thông tin đã cho trong đề bài. Sau đó, có thể sử dụng hàm số để tính toán các giá trị cần tìm hoặc để kiểm tra các điều kiện đã cho.
Giả sử đề bài yêu cầu xác định hàm số biểu diễn chi phí vận chuyển hàng hóa theo quãng đường vận chuyển. Nếu chi phí cố định là 50.000 đồng và chi phí cho mỗi km là 10.000 đồng, thì hàm số biểu diễn chi phí vận chuyển (y) theo quãng đường vận chuyển (x) sẽ là y = 10.000x + 50.000.
Để củng cố kiến thức và kỹ năng giải bài tập hàm số bậc nhất, các em học sinh nên luyện tập thêm với các bài tập tương tự. Có rất nhiều nguồn tài liệu tham khảo khác nhau, bao gồm sách giáo khoa, sách bài tập, các trang web học toán online và các video hướng dẫn trên YouTube.
Hàm số bậc nhất có rất nhiều ứng dụng trong thực tế, chẳng hạn như trong kinh tế, tài chính, vật lý, kỹ thuật và khoa học máy tính. Ví dụ, hàm số bậc nhất có thể được sử dụng để mô tả mối quan hệ giữa giá cả và nhu cầu, giữa nhiệt độ và áp suất, hoặc giữa thời gian và quãng đường.
Giaitoan.edu.vn là một trang web học toán online uy tín, cung cấp lời giải chi tiết, dễ hiểu cho các bài tập Toán 8 Kết nối tri thức. Chúng tôi luôn cố gắng cập nhật nội dung mới nhất và cung cấp các phương pháp giải bài tập hiệu quả nhất, giúp các em học sinh học Toán 8 một cách dễ dàng và thú vị.
| Công thức | Mô tả |
|---|---|
| y = ax + b | Dạng tổng quát của hàm số bậc nhất |
| a | Hệ số góc |
| b | Giao điểm với trục tung |
Hy vọng với hướng dẫn chi tiết này, các em học sinh sẽ tự tin giải bài 3.23 trang 42 sách bài tập Toán 8 Kết nối tri thức và đạt kết quả tốt trong môn Toán.