Bài 9.44 trang 63 Sách bài tập Toán 8 - Kết nối tri thức là một bài tập quan trọng trong chương trình học Toán 8. Bài tập này yêu cầu học sinh vận dụng kiến thức về các định lý đã học để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 9.44 trang 63 Sách bài tập Toán 8 - Kết nối tri thức, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
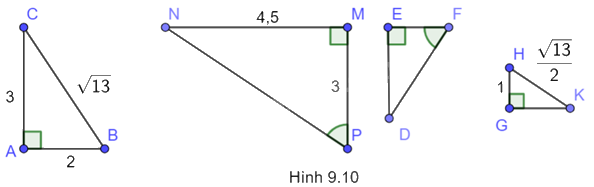
Hãy liệt kê ba cặp tam giác vuông trong Hình 9.10 đồng dạng và giải thích chúng đồng dạng dựa theo trường hợp nào của hai tam giác vuông đồng dạng?
Đề bài
Hãy liệt kê ba cặp tam giác vuông trong Hình 9.10 đồng dạng và giải thích chúng đồng dạng dựa theo trường hợp nào của hai tam giác vuông đồng dạng?
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức các trường hợp đồng dạng của tam giác vuông để tìm các tam giác đồng dạng:
+ Nếu một góc nhọn của tam giác vuông này bằng một góc nhọn của tam giác vuông kia thì hai tam giác vuông đó đồng dạng với nhau.
+ Nếu hai cạnh góc vuông của tam giác vuông này tỉ lệ với hai cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó đồng dạng với nhau.
+ Nếu cạnh huyền và một cạnh góc vuông của tam giác vuông này tỉ lệ với cạnh huyền và một cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó đồng dạng với nhau.
Lời giải chi tiết
Tam giác ABC và tam giác MPN có: \(\widehat A = \widehat M = {90^0},\frac{{AB}}{{MP}} = \frac{{AC}}{{NM}}\left( {do\;\frac{2}{3} = \frac{3}{{4,5}}} \right)\)
Do đó, $\Delta ABC\backsim \Delta MPN\left( cgv-cgv \right)$
Tam giác MNP và tam giác EDF có: \(\widehat M = \widehat E = {90^0},\widehat P = \widehat F\). Do đó, $\Delta MPN\backsim \Delta EFD\left( g-g \right)$
Tam giác ABC và tam giác GHK có: \(\widehat A = \widehat G = {90^0},\frac{{AB}}{{GH}} = \frac{{BC}}{{HK}}\left( {do\;\frac{2}{1} = \frac{{\sqrt {13} }}{{\frac{{\sqrt {13} }}{2}}}} \right)\)
Do đó, $\Delta ABC\backsim \Delta GHK\left( ch-cgv \right)$
Bài 9.44 trang 63 Sách bài tập Toán 8 - Kết nối tri thức thuộc chương trình học Toán 8, tập trung vào việc vận dụng các kiến thức về hình học, đặc biệt là các định lý liên quan đến tứ giác và các tính chất của đường trung bình trong tam giác. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững lý thuyết và biết cách áp dụng vào thực tế.
(Nội dung đề bài sẽ được chèn vào đây - ví dụ: Cho hình bình hành ABCD, gọi E là trung điểm của CD. Gọi F là giao điểm của AE và BD. Chứng minh rằng DF = 1/2 BF.)
Để giải bài toán này, chúng ta sẽ sử dụng các bước sau:
Chứng minh:
Vì ABCD là hình bình hành nên AB // CD và AB = CD. Do E là trung điểm của CD nên DE = EC = 1/2 CD = 1/2 AB.
Xét tam giác ABE và tam giác FDE, ta có:
Do đó, tam giác ABE đồng dạng với tam giác FDE (g-g). Suy ra:
DF/BF = DE/AB = (1/2 AB)/AB = 1/2
Vậy DF = 1/2 BF (điều phải chứng minh).
Ngoài bài 9.44, còn rất nhiều bài tập tương tự trong chương trình Toán 8 yêu cầu học sinh vận dụng kiến thức về hình học. Để giải các bài tập này, bạn có thể áp dụng các phương pháp sau:
Để củng cố kiến thức và rèn luyện kỹ năng giải toán, bạn nên luyện tập thêm các bài tập khác trong sách bài tập Toán 8 - Kết nối tri thức. Ngoài ra, bạn có thể tìm kiếm các bài tập tương tự trên internet hoặc tham gia các khóa học toán online.
Bài 9.44 trang 63 Sách bài tập Toán 8 - Kết nối tri thức là một bài tập quan trọng giúp học sinh hiểu sâu hơn về các kiến thức hình học. Hy vọng với lời giải chi tiết và hướng dẫn giải bài tập trên, các em học sinh sẽ tự tin hơn trong việc học Toán 8.
Giaitoan.edu.vn luôn đồng hành cùng các em học sinh trên con đường chinh phục tri thức. Chúc các em học tập tốt!