Bài 9.17 trang 55 sách bài tập Toán 8 thuộc chương trình Kết nối tri thức với cuộc sống là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng áp dụng kiến thức về hình hộp chữ nhật và hình lập phương vào giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 9.17, giúp các em học sinh nắm vững phương pháp giải và tự tin hơn trong các bài kiểm tra.
Cho tứ giác ABCD với \(AB = 2cm,AD = 3cm,BD = 4cm,BC = 6cm,CD = 8cm\). Chứng minh rằng $\Delta ABD\backsim \Delta BDC$ và AB song song với CD.
Đề bài
Cho tứ giác ABCD với \(AB = 2cm,AD = 3cm,BD = 4cm,BC = 6cm,CD = 8cm\). Chứng minh rằng $\Delta ABD\backsim \Delta BDC$ và AB song song với CD.
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức về định lý (trường hợp đồng dạng cạnh – cạnh – cạnh) để chứng minh hai tam giác đồng dạng: Nếu ba cạnh của tam giác này tỉ lệ với ba cạnh của tam giác kia thì hai tam giác đó đồng dạng với nhau.
Lời giải chi tiết
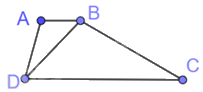
Tam giác ABD và tam giác BDC có:
\(\frac{{AB}}{{BD}} = \frac{{BD}}{{DC}} = \frac{{AD}}{{BC}}\left( {do\frac{2}{4} = \frac{4}{8} = \frac{3}{6}} \right)\)
Do đó, $\Delta ABD\backsim \Delta BDC$ (c.c.c)
Suy ra: \(\widehat {ABD} = \widehat {BDC}\) (hai góc tương ứng)
Mà hai góc này ở vị trí so le trong. Do đó, AB//CD.
Bài 9.17 yêu cầu học sinh vận dụng kiến thức về thể tích hình hộp chữ nhật và hình lập phương để giải quyết một bài toán thực tế liên quan đến việc tính toán lượng nước cần thiết để đổ đầy một bể bơi hình hộp chữ nhật.
Đề bài: Một bể bơi hình hộp chữ nhật có chiều dài 10m, chiều rộng 6m và chiều sâu 1,5m. Tính thể tích nước cần thiết để đổ đầy bể.
Giải:
Thể tích của bể bơi hình hộp chữ nhật là:
V = chiều dài x chiều rộng x chiều sâu = 10m x 6m x 1,5m = 90m3
Vậy, thể tích nước cần thiết để đổ đầy bể là 90m3.
Để củng cố kiến thức về thể tích hình hộp chữ nhật và hình lập phương, các em có thể tự giải các bài tập sau:
Khi giải các bài tập về thể tích, các em cần chú ý đến các yếu tố sau:
Bài 9.17 trang 55 sách bài tập Toán 8 - Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng áp dụng kiến thức về thể tích hình hộp chữ nhật và hình lập phương vào giải quyết các bài toán thực tế. Hy vọng với lời giải chi tiết và những lưu ý trên, các em học sinh sẽ tự tin hơn trong việc giải các bài tập tương tự.
| Hình | Công thức |
|---|---|
| Hình hộp chữ nhật | V = a.b.c |
| Hình lập phương | V = a3 |
| Trong đó: a, b, c là các kích thước của hình; V là thể tích. | |