Bài 3.30 trang 44 sách bài tập Toán 8 Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng giải bài toán thực tế liên quan đến các ứng dụng của tam giác đồng dạng. Bài tập này thường yêu cầu học sinh vận dụng kiến thức về tỉ lệ thức, tam giác đồng dạng để giải quyết các vấn đề về chiều cao, khoảng cách.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 3.30 trang 44 sách bài tập Toán 8 Kết nối tri thức, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Khái niệm tam giác, tứ giác có thể mở rộng thành khái niệm n – giác (n là số tự nhiên lớn hơn 2) như sau:
Đề bài
Khái niệm tam giác, tứ giác có thể mở rộng thành khái niệm n – giác (n là số tự nhiên lớn hơn 2) như sau:
n – giác là hình tạo bởi n đoạn thẳng (gọi là cạnh của n – giác) \({A_0}{A_1},{A_1}{A_2},...,{A_{n - 1}}{A_n},{A_n}{A_0}\) (các điểm \({A_0},{A_1},...,{A_n}\) gọi là đỉnh của n – giác), trong đó không có ba đỉnh nào cùng nằm trên một đường thẳng và hình nằm về một phía đối với mỗi đường thẳng chứa một cạnh.
Khi \(n = 3;4;5;6;7;8,\) n – giác còn được gọi lần lượt là tam giác, tứ giác, ngũ giác, lục giác, thất giác, bát giác.
Hai đỉnh của n – giác gọi là kề nhau nếu chúng là hai đỉnh của một cạnh của n – giác.
Đoạn thẳng nối hai đỉnh không kề nhau của n – giác gọi là một đường chéo của n – giác.
a) Chứng minh qua mỗi đỉnh của n – giác, có \(n - 3\) đường chéo của n – giác. Từ đó suy ra n – giác có \(\frac{{n\left( {n - 3} \right)}}{2}\) đường chéo.
b) Hãy vẽ tất cả các đường chéo của một ngũ giác \(\left( {n = 5} \right)\)
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức về đường chéo của đa giác để chứng minh: Đoạn thẳng nối hai đỉnh không kề nhau của n – giác gọi là một đường chéo của n – giác.
Lời giải chi tiết
a) Không có đường chéo nào của n – giác nối một đỉnh cho trước với chính đỉnh đó và với hai đỉnh kề với đỉnh đó nên có \(n - 3\) đường chéo của n – giác qua đỉnh đang xét.
Tính theo cách đó thì n – giác có \(n\left( {n - 3} \right)\) đường chéo, nhưng mỗi đường chéo được tính hai lần nên n – giác có tất cả \(\frac{{n\left( {n - 3} \right)}}{2}\) đường chéo.
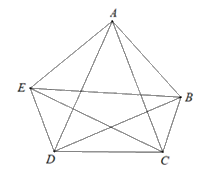
b) Giả sử ta có ngũ giác ABCDE, khi đó ngũ giác này có \(\frac{{5\left( {5 - 3} \right)}}{2} = 5\) đường chéo, đó là: AC, AD, BD, BE, CE.
Bài 3.30 trang 44 sách bài tập Toán 8 Kết nối tri thức yêu cầu học sinh giải quyết một bài toán thực tế liên quan đến việc tính chiều cao của một vật thể dựa trên bóng của nó và góc tạo bởi tia nắng mặt trời. Để giải bài toán này, học sinh cần nắm vững kiến thức về tam giác đồng dạng và các tính chất liên quan.
Trước khi đi vào giải bài toán, chúng ta cần phân tích đề bài để xác định các yếu tố quan trọng. Bài toán thường cho trước chiều cao của một vật thể, chiều dài bóng của vật thể đó, và góc tạo bởi tia nắng mặt trời. Yêu cầu của bài toán là tính chiều cao của một vật thể khác dựa trên chiều dài bóng của nó và góc tạo bởi tia nắng mặt trời.
Để giải bài toán này, chúng ta có thể sử dụng kiến thức về tam giác đồng dạng. Cụ thể, chúng ta có thể xây dựng một tam giác vuông có cạnh góc vuông là chiều cao của vật thể và chiều dài bóng của vật thể. Sau đó, chúng ta có thể sử dụng tỉ lệ thức để tính chiều cao của vật thể cần tìm.
Dưới đây là lời giải chi tiết bài 3.30 trang 44 sách bài tập Toán 8 Kết nối tri thức:
Ví dụ, giả sử chúng ta có một cột điện cao 6m và bóng của nó dài 8m. Góc tạo bởi tia nắng mặt trời là 30 độ. Chúng ta muốn tính chiều cao của một tòa nhà có bóng dài 20m. Chúng ta có thể sử dụng tỉ lệ thức sau:
Chiều cao cột điện / Chiều dài bóng cột điện = Chiều cao tòa nhà / Chiều dài bóng tòa nhà
6 / 8 = Chiều cao tòa nhà / 20
Chiều cao tòa nhà = (6 * 20) / 8 = 15m
Để rèn luyện kỹ năng giải bài toán này, bạn có thể thử giải các bài tập tương tự. Ví dụ:
Bài 3.30 trang 44 sách bài tập Toán 8 Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng giải bài toán thực tế liên quan đến tam giác đồng dạng. Bằng cách nắm vững kiến thức và áp dụng đúng các phương pháp giải, học sinh có thể tự tin giải quyết các bài toán tương tự.
Giaitoan.edu.vn hy vọng rằng lời giải chi tiết này sẽ giúp các em học sinh hiểu rõ hơn về bài toán và đạt kết quả tốt trong học tập.