Bài 9.23 trang 56 sách bài tập Toán 8 Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về ứng dụng thực tế của phương trình bậc nhất một ẩn. Bài tập này thường yêu cầu học sinh xây dựng phương trình từ một tình huống cụ thể và giải phương trình để tìm ra nghiệm.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 9.23 trang 56, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Cho tam giác ABC và hai điểm M, N lần lượt nằm trên AB, AC sao cho MN song song với BC.
Đề bài
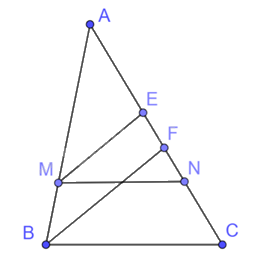
Cho tam giác ABC và hai điểm M, N lần lượt nằm trên AB, AC sao cho MN song song với BC. Gọi ME, BF lần lượt là phân giác của các góc M, B của các tam giác AMN và tam giác ABC. Chứng minh rằng:
a) $\Delta MEN\backsim \Delta BFC$
b) \(\frac{{AE}}{{AF}} = \frac{{MN}}{{BC}}\)
Phương pháp giải - Xem chi tiết
a) Sử dụng kiến thức về định lý (trường hợp đồng dạng góc – góc) để chứng minh hai tam giác đồng dạng: Nếu hai góc của tam giác lần lượt bằng hai góc của tam giác kia thì hai tam giác đó đồng dạng với nhau.
b) + Sử dụng kiến thức hệ quả định lý Thalès: Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại thì nó tạo thành một tam giác mới có ba cạnh tương ứng tỉ lệ với ba cạnh của tam giác đã cho.
+ Sử dụng tính chất đường phân giác của tam giác: Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn tỉ lệ với hai cạnh kề của hai đoạn ấy.
Lời giải chi tiết
a) Vì MN//BC (gt) nên
+ \(\widehat {ENM} = \widehat C\) (hai góc đồng vị)
+ \(\widehat {AMN} = \widehat {ABC}\) (hai góc đồng vị)
Mà ME, BF lần lượt là phân giác của các góc M, B của các tam giác AMN và tam giác ABC nên \(\widehat {EMN} = \frac{1}{2}\widehat {AMN} = \frac{1}{2}\widehat {ABC} = \widehat {FBC}\)
Tam giác MEN và tam giác BFC có:
\(\widehat {ENM} = \widehat C\) (cmt), \(\widehat {EMN} = \widehat {FBC}\) (cmt)
Do đó, $\Delta MEN\backsim \Delta BFC\left( g-g \right)$
b) Tam giác ABC có: MN//BC nên theo hệ quả định lý Thalès ta có: \(\frac{{MN}}{{BC}} = \frac{{AM}}{{AB}}\) (1)
Vì ME, BF lần lượt là phân giác của các góc M, B của các tam giác AMN và tam giác ABC nên \(\widehat {EMA} = \frac{1}{2}\widehat {AMN} = \frac{1}{2}\widehat {ABC} = \widehat {FBA}\)
Do đó, \(\widehat {EMA} = \widehat {FBA}\), mà hai góc này ở vị trí đồng vị nên ME//BF.
Tam giác ABF có: ME//BF nên theo hệ quả định lý Thalès ta có: \(\frac{{AE}}{{AF}} = \frac{{AM}}{{AB}}\) (2)
Từ (1) và (2) ta có: \(\frac{{AE}}{{AF}} = \frac{{MN}}{{BC}}\)
Bài 9.23 sách bài tập Toán 8 Kết nối tri thức yêu cầu học sinh giải quyết một bài toán thực tế liên quan đến việc tính toán chi phí và lợi nhuận. Để giải bài toán này, chúng ta cần hiểu rõ các khái niệm về phương trình bậc nhất một ẩn và cách xây dựng phương trình từ các thông tin đã cho.
Một người mua 10 kg cam với giá 30 000 đồng/kg. Người đó đem bán với giá 40 000 đồng/kg. Hỏi người đó lãi bao nhiêu tiền?
Bài toán này yêu cầu chúng ta tính toán lợi nhuận của người bán cam. Lợi nhuận được tính bằng hiệu giữa doanh thu và chi phí. Doanh thu là số tiền người bán cam thu được từ việc bán cam, còn chi phí là số tiền người bán cam bỏ ra để mua cam.
Bước 1: Tính chi phí mua cam
Chi phí mua cam là: 10 kg * 30 000 đồng/kg = 300 000 đồng
Bước 2: Tính doanh thu từ việc bán cam
Doanh thu từ việc bán cam là: 10 kg * 40 000 đồng/kg = 400 000 đồng
Bước 3: Tính lợi nhuận
Lợi nhuận là: 400 000 đồng - 300 000 đồng = 100 000 đồng
Kết luận: Người đó lãi 100 000 đồng.
Trong bài toán này, chúng ta có thể đặt x là lợi nhuận của người bán cam. Khi đó, ta có phương trình:
x = Doanh thu - Chi phí
x = (10 * 40 000) - (10 * 30 000)
x = 400 000 - 300 000
x = 100 000
Vậy, lợi nhuận của người bán cam là 100 000 đồng.
Để rèn luyện kỹ năng giải các bài toán tương tự, các em có thể tham khảo các bài tập sau:
Phương trình bậc nhất một ẩn có rất nhiều ứng dụng trong thực tế, ví dụ như:
Bài 9.23 trang 56 sách bài tập Toán 8 Kết nối tri thức là một bài tập đơn giản nhưng quan trọng, giúp học sinh rèn luyện kỹ năng về ứng dụng thực tế của phương trình bậc nhất một ẩn. Hy vọng với lời giải chi tiết và dễ hiểu trên đây, các em học sinh sẽ nắm vững kiến thức và tự tin giải các bài tập tương tự.
| Đại lượng | Giá trị |
|---|---|
| Số kg cam mua | 10 kg |
| Giá mua cam (đồng/kg) | 30 000 đồng/kg |
| Giá bán cam (đồng/kg) | 40 000 đồng/kg |
| Lợi nhuận (đồng) | 100 000 đồng |