Bài 3.10 trang 34 sách bài tập Toán 8 thuộc chương 3: Các góc tạo bởi một đường thẳng cắt hai đường thẳng. Bài tập này yêu cầu học sinh vận dụng kiến thức về các góc so le trong, đồng vị, trong cùng phía để chứng minh tính chất của các góc.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 3.10 trang 34 sách bài tập Toán 8 - Kết nối tri thức với cuộc sống, giúp các em học sinh nắm vững kiến thức và rèn luyện kỹ năng giải bài tập.
Cho hình thang cân ABCD với hai đường thẳng chứa hai cạnh bên AD, BC cắt nhau tại S.
Đề bài
Cho hình thang cân ABCD với hai đường thẳng chứa hai cạnh bên AD, BC cắt nhau tại S. Gọi O là giao điểm của hai đường chéo AC và BD. Chứng minh đường thẳng SO đi qua trung điểm của AB, đi qua trung điểm của CD.
Phương pháp giải - Xem chi tiết
Sử dụng tính chất của hình thang cân, tam giác cân, đường trung trực.
Lời giải chi tiết
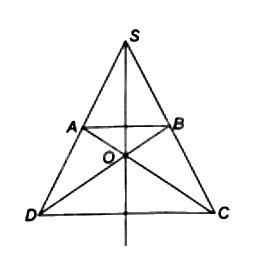
Do ABCD là hình thang cân nên AD = BC, AC = BD, \(\widehat {ADC} = \widehat {BCD}\)
Xét \(\Delta ABC\) và \(\Delta BAD\) có
\(BC = AD,AC = BD\)
Cạnh AB chung
Do đó \(\Delta ABC = \Delta BAD\) (c.c.c)
Suy ra \(\widehat {BAC} = \widehat {ABD}\).
Từ đó \(\Delta OAB\) là tam giác cân tại O, nên \(OA = OB.\)
Ta có: \(OA + OC = AC\);\(OB + OD = BD\) , mà \(OA = OB,AC = BD\)
Suy ra \(OC = OD\)
Do đó O cách đều A và B; O cách đều C và D;
Do \(AB//CD\) nên \(\widehat {SAB} = \widehat {SDC}\); \(\widehat {SBA} = \widehat {SCD}\) (các cặp góc ở vị trí đồng vị)
Mà \(\widehat {ADC} = \widehat {BCD}\) hay \(\widehat {SDC} = \widehat {SCD}\)
suy ra \(\widehat {SAB} = \widehat {SDC} = \widehat {SBA} = \widehat {SCD}\).
Suy ra là \(\Delta SAB\), \(\Delta SCD\) các tam giác cân tại đỉnh S nên \(SA = SB,SC = SD\)
Do đó S cũng cách đều A và B, cách đều C và D.
Vậy S và O cùng nằm trên đường trung trực của AB, của CD nên đường thẳng SO đi qua trung điểm của AB, CD.
Bài 3.10 trang 34 sách bài tập Toán 8 - Kết nối tri thức là một bài tập quan trọng giúp học sinh củng cố kiến thức về các góc tạo bởi một đường thẳng cắt hai đường thẳng. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững các khái niệm và tính chất sau:
Đề bài: (Nội dung đề bài sẽ được chèn vào đây - ví dụ: Cho hình vẽ, biết a // b. Tính số đo góc x.)
Lời giải:
(Giải thích chi tiết từng bước giải, kèm theo hình vẽ minh họa nếu cần thiết. Ví dụ: Vì a // b nên góc A1 = góc B1 (so le trong). Ta có góc A1 = 60 độ, suy ra góc B1 = 60 độ. Góc x là góc kề bù với góc B1, nên góc x = 180 độ - 60 độ = 120 độ.)
Để hiểu rõ hơn về cách giải bài tập về các góc tạo bởi một đường thẳng cắt hai đường thẳng, chúng ta cùng xem xét một số ví dụ minh họa sau:
Ngoài ra, các em có thể tự luyện tập với các bài tập tương tự sau:
Để giải bài tập về các góc tạo bởi một đường thẳng cắt hai đường thẳng một cách nhanh chóng và chính xác, các em có thể áp dụng một số mẹo sau:
Bài 3.10 trang 34 sách bài tập Toán 8 - Kết nối tri thức là một bài tập quan trọng giúp học sinh củng cố kiến thức về các góc tạo bởi một đường thẳng cắt hai đường thẳng. Hy vọng với lời giải chi tiết và các ví dụ minh họa trên, các em học sinh sẽ nắm vững kiến thức và rèn luyện kỹ năng giải bài tập một cách hiệu quả.