Bài 12 trang 82 sách bài tập Toán 8 Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng giải toán thực tế. Bài tập này thường liên quan đến các ứng dụng của định lý Thales trong hình học.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 12 trang 82, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Cho tam giác ABC có đường cao AH. Lấy E, F lần lượt trên AB, AC sao cho HE, HF lần lượt vuông góc với AB, AC.
Đề bài
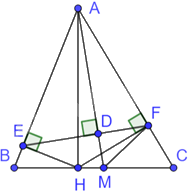
Cho tam giác ABC có đường cao AH. Lấy E, F lần lượt trên AB, AC sao cho HE, HF lần lượt vuông góc với AB, AC. Lấy điểm D trên EF sao cho AD vuông góc với EF. Đường thẳng AD cắt BC tại M. Chứng minh rằng:
a) \(AE.AB = AF.AC\)
b) $\Delta ADE\backsim \Delta AHC$ và $\Delta ANF\backsim \Delta AMB$ ($\Delta ANF\backsim \Delta AMB$ không chứng minh được vì đề bài không cho vị trí của điểm N).
Phương pháp giải - Xem chi tiết
a) Sử dụng kiến thức về định lý (trường hợp đồng dạng góc – góc) để chứng minh: Nếu hai góc của tam giác lần lượt bằng hai góc của tam giác kia thì hai tam giác đó đồng dạng với nhau.
b) + Sử dụng kiến thức về định lý (trường hợp đồng dạng cạnh – góc – cạnh) để chứng minh: Nếu hai cạnh của tam giác này tỉ lệ với hai cạnh của tam giác kia và góc tạo bởi các cặp cạnh đó bằng nhau thì hai tam giác đó đồng dạng với nhau.
+ Sử dụng kiến thức về định lý (trường hợp đồng dạng góc – góc) để chứng minh: Nếu hai góc của tam giác lần lượt bằng hai góc của tam giác kia thì hai tam giác đó đồng dạng với nhau.
Lời giải chi tiết
a) Vì AH là đường cao của tam giác ABC nên \(\widehat {AHB} = \widehat {AHC} = {90^0}\)
Vì HE, HF lần lượt vuông góc với AB, AC nên \(HE \bot AB,HF \bot AC\)
Do đó, \(\widehat {HEB} = \widehat {HEA} = \widehat {HFA} = \widehat {HFC} = {90^0}\)
Tam giác HEA và tam giác BHA có:
\(\widehat {HEA} = \widehat {AHB} = {90^0},\widehat {BAH}\;chung\)
Do đó, $\Delta HEA\backsim \Delta BHA\left( g-g \right)$
Suy ra: \(\frac{{AE}}{{AH}} = \frac{{AH}}{{AB}}\) nên \(AE.AB = A{H^2}\left( 1 \right)\)
Tam giác HFA và tam giác CHA có:
\(\widehat {HFA} = \widehat {AHC} = {90^0},\widehat {CAH}\;chung\)
Do đó, $\Delta HFA\backsim \Delta CHA\left( g-g \right)$
Suy ra: \(\frac{{AF}}{{AH}} = \frac{{AH}}{{AC}}\) nên \(AF.AC = A{H^2}\left( 2 \right)\)
Từ (1) và (2) ta có: \(AE.AB = AF.AC\)
b) Vì \(AE.AB = AF.AC\) nên \(\frac{{AE}}{{AC}} = \frac{{AF}}{{AB}}\)
Tam giác AEF và tam giác ACB có: \(\frac{{AE}}{{AC}} = \frac{{AF}}{{AB}},\widehat {BAC}\;chung\)
Do đó, $\Delta AEF\backsim \Delta ACB\left( c-g-c \right)$, suy ra, \(\widehat {AEF} = \widehat C\)
Tam giác AED và tam giác ACH có:
\(\widehat {ADE} = \widehat {AHC} = {90^0},\widehat {AEF} = \widehat C\left( {cmt} \right)\)
Do đó, $\Delta ADE\backsim \Delta AHC\left( g-g \right)$
Bài 12 trang 82 sách bài tập Toán 8 Kết nối tri thức yêu cầu học sinh vận dụng kiến thức về định lý Thales để giải quyết một bài toán thực tế liên quan đến việc chia tỉ lệ trên đoạn thẳng. Để giải bài tập này một cách hiệu quả, chúng ta cần nắm vững các bước sau:
Giả sử bài toán yêu cầu tính độ dài đoạn thẳng MN, biết rằng đường thẳng MN song song với cạnh BC của tam giác ABC, và các đoạn thẳng AM, MB có độ dài lần lượt là 2cm và 3cm. Theo định lý Thales, ta có:
AM / AB = AN / AC = MN / BC
Trong đó, AB = AM + MB = 2cm + 3cm = 5cm. Nếu AC = 4cm và BC = 6cm, ta có thể tính MN như sau:
MN / BC = AM / AB
MN / 6cm = 2cm / 5cm
MN = (2cm / 5cm) * 6cm = 2.4cm
Vậy, độ dài đoạn thẳng MN là 2.4cm.
Ngoài bài 12 trang 82, sách bài tập Toán 8 Kết nối tri thức còn nhiều bài tập tương tự yêu cầu vận dụng định lý Thales. Các bài tập này có thể khác nhau về hình vẽ và số liệu, nhưng phương pháp giải cơ bản vẫn là:
Để nắm vững kiến thức về định lý Thales và rèn luyện kỹ năng giải bài tập, các em học sinh có thể tham khảo thêm các tài liệu sau:
Bài 12 trang 82 sách bài tập Toán 8 Kết nối tri thức là một bài tập quan trọng giúp học sinh hiểu sâu hơn về định lý Thales và ứng dụng của nó trong thực tế. Bằng cách nắm vững các bước giải và luyện tập thường xuyên, các em học sinh có thể tự tin giải quyết các bài tập tương tự và đạt kết quả tốt trong môn Toán.