Bài 9.65 trang 69 sách bài tập Toán 8 thuộc chương trình Kết nối tri thức với cuộc sống là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng giải bài toán thực tế liên quan đến ứng dụng của hàm số bậc nhất.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 9.65 này, giúp các em học sinh nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Chúng tôi luôn cố gắng cung cấp những giải pháp học tập tốt nhất, hỗ trợ các em học sinh chinh phục môn Toán một cách hiệu quả.
Cho tam giác ABC vuông tại A \(\left( {AC > AB} \right)\), có AD là đường phân giác của góc A (D thuộc BC)
Đề bài
Cho tam giác ABC vuông tại A \(\left( {AC > AB} \right)\), có AD là đường phân giác của góc A (D thuộc BC). Qua D vẽ đường thẳng vuông góc với BC cắt cạnh AC tại E và cắt tia BA tại F. Chứng minh rằng:
a) $\Delta BDF\backsim \Delta EDC$
b) \(BD = DE\)
Phương pháp giải - Xem chi tiết
a) Sử dụng kiến thức các trường hợp đồng dạng của tam giác vuông chứng minh tam giác đồng dạng: Nếu một góc nhọn của tam giác vuông này bằng một góc nhọn của tam giác vuông kia thì hai tam giác vuông đó đồng dạng với nhau.
b) + Sử dụng kiến thức các trường hợp đồng dạng của tam giác vuông chứng minh tam giác đồng dạng: Nếu một góc nhọn của tam giác vuông này bằng một góc nhọn của tam giác vuông kia thì hai tam giác vuông đó đồng dạng với nhau.
+ Sử dụng tính chất phân giác trong tam giác: Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề hai đoạn thẳng ấy.
Lời giải chi tiết
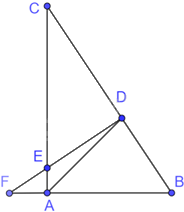
a) Vì FD vuông góc với CB tại D nên \(\widehat {FDB} = \widehat {EDC} = {90^0}\).
Tam giác FBD và tam giác CED có:
\(\widehat {FDB} = \widehat {EDC} = {90^0}\), \(\widehat F = \widehat C\left( { = {{90}^0} - \widehat B} \right)\)
Do đó, $\Delta BDF\backsim \Delta EDC\left( g-g \right)$
b) Tam giác ABC và tam giác DEC có:
\(\widehat {BAC} = \widehat {EDC} = {90^0},\widehat C\;chung\)
Do đó, $\Delta ABC\backsim \Delta DEC\left( g-g \right)$. Suy ra, \(\frac{{AB}}{{DE}} = \frac{{AC}}{{DC}}\)
Vì AD là phân giác của góc BAC trong tam giác ABC nên \(\frac{{BD}}{{DC}} = \frac{{AB}}{{AC}}\), suy ra \(\frac{{AC}}{{DC}} = \frac{{AB}}{{BD}}\)
Do đó: \(\frac{{AB}}{{DE}} = \frac{{AB}}{{BD}}\). Suy ra \(BD = DE\)
Bài 9.65 trang 69 sách bài tập Toán 8 - Kết nối tri thức với cuộc sống là một bài toán ứng dụng thực tế, yêu cầu học sinh vận dụng kiến thức về hàm số bậc nhất để giải quyết một tình huống cụ thể. Để hiểu rõ hơn về bài toán này, chúng ta sẽ cùng nhau phân tích đề bài, xác định các yếu tố quan trọng và đưa ra lời giải chi tiết.
Đề bài yêu cầu chúng ta giải quyết một vấn đề liên quan đến việc tính toán chi phí vận chuyển hàng hóa. Cụ thể, một công ty vận tải tính phí vận chuyển theo công thức hàm số bậc nhất. Chúng ta cần xác định hệ số của hàm số này dựa trên các thông tin được cung cấp trong đề bài.
Để giải bài toán này, chúng ta cần thực hiện các bước sau:
Ví dụ, giả sử đề bài cho biết:
Chúng ta có thể lập hệ phương trình sau:
5a + b = 50.000
10a + b = 80.000
Giải hệ phương trình này, ta được a = 30.000 và b = -100.000. Vậy hàm số bậc nhất có dạng y = 30.000x - 100.000.
Khi giải bài toán ứng dụng, điều quan trọng là phải hiểu rõ ý nghĩa của các biến và hệ số trong hàm số. Điều này sẽ giúp chúng ta áp dụng kiến thức một cách linh hoạt và giải quyết các vấn đề thực tế một cách hiệu quả.
Ngoài bài 9.65, các em học sinh có thể tìm hiểu thêm về các ứng dụng khác của hàm số bậc nhất trong đời sống, chẳng hạn như tính tiền điện, tiền nước, hoặc tính lãi suất ngân hàng. Việc nắm vững kiến thức về hàm số bậc nhất sẽ giúp các em giải quyết nhiều vấn đề thực tế một cách dễ dàng hơn.
Để củng cố kiến thức, các em có thể tự giải thêm các bài tập tương tự trong sách bài tập Toán 8 - Kết nối tri thức với cuộc sống. Ngoài ra, các em cũng có thể tìm kiếm các bài tập trực tuyến trên các trang web học toán uy tín.
Bài 9.65 trang 69 sách bài tập Toán 8 - Kết nối tri thức với cuộc sống là một bài toán ứng dụng thực tế, giúp học sinh rèn luyện kỹ năng giải bài toán và vận dụng kiến thức về hàm số bậc nhất. Hy vọng rằng với lời giải chi tiết và những lưu ý quan trọng mà chúng tôi đã cung cấp, các em học sinh sẽ hiểu rõ hơn về bài toán này và tự tin hơn trong quá trình học tập.