Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 8. Bài viết này sẽ hướng dẫn bạn cách giải bài 14 trang 83 Sách bài tập Toán 8 - Kết nối tri thức một cách nhanh chóng và hiệu quả.
Chúng tôi luôn cố gắng mang đến những phương pháp giải toán đơn giản, dễ tiếp thu, giúp các em học sinh nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy \(AB = 10cm,\) cạnh bên \(SD = 15cm\).
Đề bài
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy \(AB = 10cm,\) cạnh bên \(SD = 15cm\). Gọi O là giao điểm của AC và BD, M và N lần lượt là trung điểm của AB và CD.
a) Chứng minh \(SO \bot MN.\) Từ đó tính độ dài đường cao SO của hình chóp.
b) Tính thể tích của hình chóp.
c) Tính diện tích toàn phần của hình chóp.
Phương pháp giải - Xem chi tiết
a) - Sử dụng kiến thức về hình chóp tứ giác đều hình chóp tứ giác đều: Hình chóp tứ giác đều có:
+ Mặt đáy là hình vuông.
+ Mặt bên là các tam giác cân bằng nhau có chung một đỉnh.
+ Đoạn thẳng nối đỉnh của hình chóp và giao điểm của hai đường chéo của mặt đáy gọi là đường cao của hình chóp tứ giác đều.
+ Đường cao vẽ từ đỉnh của mỗi mặt bên gọi là trung đoạn của hình chóp tứ giác đều.
- Sử dụng định lí Pythagore để tính đường cao SO.
b) Sử dụng kiến thức về thể tích của hình chóp tứ giác đều để tính thể tích hình chóp: Thể tích của hình chóp tam giác đều bằng \(\frac{1}{3}\) tích của diện tích đáy với chiều cao của nó.
c) + Sử dụng kiến thức về diện tích xung quanh của hình chóp tứ giác đều để tính diện tích xung quanh hình chóp: Diện tích xung quanh của hình chóp tứ giác đều bằng tích của nửa chu vi đáy với trung đoạn.
+ Sử dụng kiến thức về diện tích toàn phần của hình chóp tứ giác đều để tính diện tích toàn phần hình chóp: Diện tích toàn phần của hình chóp tứ giác đều bằng tổng diện tích xung quanh và diện tích của mặt đáy
Lời giải chi tiết
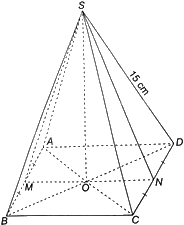
a) Vì các mặt bên của hình chóp tứ giác đều là các tam giác cân bằng nhau nên các đường trung tuyến tương ứng của chúng bằng nhau, tức là \(SM = SN\). Tam giác SMN là tam giác cân tại S và O là trung điểm của MN nên \(SO \bot MN.\)
Áp dụng định lí Pythagore vào tam giác ABC vuông tại B có: \(A{C^2} = A{B^2} + B{C^2} = 200\) nên \(AC = 10\sqrt 2 cm\)
Do đó, \(OA = \frac{1}{2}AC = 5\sqrt 2 cm\)
Áp dụng định lí Pythagore vào tam giác SOA vuông tại O có: \(A{O^2} + S{O^2} = S{A^2}\) nên \(S{O^2} = S{A^2} - A{O^2} = 175\) nên \(SO = \sqrt {175} = 5\sqrt 7 cm\)
b) Thể tích của hình chóp đều S.ABCD là:
\({V_{S.ABCD}} = \frac{1}{3}.SO.{S_{ABCD}} = \frac{1}{3}.5\sqrt 7 {.10^2} = \frac{{500\sqrt 7 }}{3}\left( {c{m^3}} \right)\)
c) Áp dụng định lí Pythagore vào tam giác SMA vuông tại M có: \(S{M^2} + A{M^2} = S{A^2}\)
Do đó, \(S{M^2} = S{A^2} - A{M^2} = 200\) nên \(SM = 10\sqrt 2 cm\)
Nửa chu vi đáy là: \(p = 20cm\)
Diện tích xung quanh của hình chóp là: \({S_{xq}} = SM.p = 10\sqrt 2 .20 = 200\sqrt 2 \left( {c{m^2}} \right)\)
Diện tích đáy ABCD là: \({S_{ABCD}} = {10^2} = 100\left( {c{m^2}} \right)\)
Diện tích toàn phần của hình chóp S.ABCD là:
\({S_{tp}} = {S_{xq}} + {S_{ABCD}} = 200\sqrt 2 + 100 = 100\left( {\sqrt 2 + 1} \right)\left( {c{m^2}} \right)\)
Bài 14 trang 83 Sách bài tập Toán 8 - Kết nối tri thức thuộc chương trình học Toán 8, tập trung vào việc vận dụng các kiến thức về hình học, cụ thể là các tính chất của hình thang cân. Bài tập này yêu cầu học sinh phải hiểu rõ các định nghĩa, định lý liên quan đến hình thang cân để có thể giải quyết một cách chính xác.
Bài 14 trang 83 thường bao gồm các dạng bài tập sau:
Để giải bài tập hình thang cân một cách hiệu quả, bạn cần:
Bài toán: Cho hình thang cân ABCD (AB // CD, AB < CD) có AD = BC. Gọi E là giao điểm của AC và BD. Chứng minh rằng AE = BE.
Giải:
Xét tam giác ADC và tam giác BCD:
Do đó, tam giác ADC = tam giác BCD (c-g-c).
Suy ra AE = BE (các cạnh tương ứng).
Khi giải bài tập hình thang cân, bạn cần chú ý đến các tính chất đặc biệt của hình thang cân, như:
Để củng cố kiến thức về hình thang cân, bạn có thể tự giải các bài tập sau:
Bài 14 trang 83 Sách bài tập Toán 8 - Kết nối tri thức là một bài tập quan trọng giúp học sinh hiểu rõ hơn về hình thang cân và các tính chất của nó. Hy vọng rằng với hướng dẫn chi tiết và các ví dụ minh họa trong bài viết này, bạn sẽ có thể giải bài tập một cách dễ dàng và hiệu quả. Chúc bạn học tốt!
| Khái niệm | Định nghĩa |
|---|---|
| Hình thang cân | Là hình thang có hai cạnh bên bằng nhau. |
| Đường cao của hình thang cân | Là đoạn vuông góc kẻ từ một đỉnh của đáy lớn xuống đáy nhỏ. |