Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 8. Bài viết này sẽ hướng dẫn bạn cách giải bài 10.18 trang 80 sách bài tập Toán 8 - Kết nối tri thức với cuộc sống một cách nhanh chóng và hiệu quả.
Chúng tôi hiểu rằng việc giải toán đôi khi có thể gặp khó khăn, đặc biệt là với những bài tập đòi hỏi sự tư duy và vận dụng kiến thức. Vì vậy, chúng tôi đã biên soạn lời giải chi tiết, kèm theo các bước giải cụ thể để giúp bạn nắm vững kiến thức và tự tin giải các bài tập tương tự.
Cho hình chóp tứ giác đều S.ABCD có thể tích bằng \(144c{m^3}\).
Đề bài
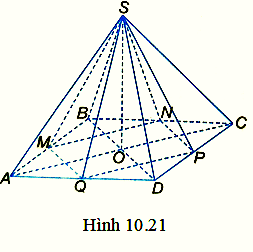
Cho hình chóp tứ giác đều S.ABCD có thể tích bằng \(144c{m^3}\). Gọi M, N, P, Q lần lượt là trung điểm của AB, BC, CD, DA (H.10.21)
Tính thể tích của hình chóp S.MNPQ.
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức về thể tích của hình chóp tứ giác đều: Thể tích của hình chóp tam giác đều bằng \(\frac{1}{3}\) tích của diện tích đáy với chiều cao của nó.
Lời giải chi tiết
Gọi O là giao điểm của AC và BD.
MN là đường trung bình của tam giác ABC nên \(MN = \frac{1}{2}AC\)
MQ là đường trung bình của tam giác ABD nên \(MQ = \frac{1}{2}BD\)
Diện tích hình vuông MNPQ là:
\({S_{MNPQ}} = \frac{1}{2}MN.MQ = \frac{1}{2}.AC.\frac{1}{2}BD = \frac{1}{2}\left( {\frac{1}{2}AC.BD} \right) = \frac{1}{2}{S_{ABCD}}\)
Hai hình chóp S.ABCD và S.MNPQ có chung chiều cao SO và \({S_{MNPQ}} = \frac{1}{2}{S_{ABCD}}\) nên \({V_{S.MNPQ}} = \frac{1}{2}{V_{S.ABCD}} = \frac{1}{2}.144 = 72\left( {c{m^3}} \right)\)
Bài 10.18 trang 80 sách bài tập Toán 8 - Kết nối tri thức với cuộc sống yêu cầu chúng ta vận dụng kiến thức về hình hộp chữ nhật và hình lập phương để giải quyết các bài toán thực tế. Dưới đây là hướng dẫn chi tiết cách giải bài tập này:
Cho hình hộp chữ nhật ABCD.EFGH có AB = 5cm, BC = 4cm, AE = 3cm.
1. Tính thể tích của hình hộp chữ nhật:
Thể tích của hình hộp chữ nhật được tính theo công thức: V = AB * BC * AE
Thay số: V = 5cm * 4cm * 3cm = 60cm3
Vậy thể tích của hình hộp chữ nhật ABCD.EFGH là 60cm3.
2. Tính diện tích xung quanh của hình hộp chữ nhật:
Diện tích xung quanh của hình hộp chữ nhật được tính theo công thức: Sxq = 2 * (AB + BC) * AE
Thay số: Sxq = 2 * (5cm + 4cm) * 3cm = 2 * 9cm * 3cm = 54cm2
Vậy diện tích xung quanh của hình hộp chữ nhật ABCD.EFGH là 54cm2.
3. Tính độ dài đường chéo AC của mặt đáy ABCD:
Mặt đáy ABCD là hình chữ nhật. Áp dụng định lý Pitago trong tam giác vuông ABC, ta có:
AC2 = AB2 + BC2
Thay số: AC2 = 52 + 42 = 25 + 16 = 41
Suy ra: AC = √41 cm
Vậy độ dài đường chéo AC của mặt đáy ABCD là √41 cm.
4. Tính độ dài đường chéo AG của hình hộp chữ nhật:
Áp dụng định lý Pitago trong tam giác vuông AEG, ta có:
AG2 = AE2 + EG2
Vì EG = AC = √41 cm (do ABCD.EFGH là hình hộp chữ nhật)
Thay số: AG2 = 32 + (√41)2 = 9 + 41 = 50
Suy ra: AG = √50 = 5√2 cm
Vậy độ dài đường chéo AG của hình hộp chữ nhật ABCD.EFGH là 5√2 cm.
Để củng cố kiến thức, bạn có thể tự giải các bài tập tương tự trong sách bài tập Toán 8 - Kết nối tri thức với cuộc sống. Hãy chú ý vận dụng các công thức và định lý đã học để giải quyết các bài toán một cách hiệu quả.
Giaitoan.edu.vn hy vọng bài giải này sẽ giúp bạn hiểu rõ hơn về cách giải bài 10.18 trang 80 sách bài tập Toán 8 - Kết nối tri thức với cuộc sống. Chúc bạn học tập tốt!