Chào mừng các em học sinh đến với lời giải chi tiết bài 10.19 trang 80 sách bài tập Toán 8 - Kết nối tri thức với cuộc sống. Bài viết này sẽ cung cấp phương pháp giải bài tập một cách dễ hiểu, giúp các em nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán, cung cấp các bài giải chuẩn xác và đầy đủ.
Một cái lều đồ chơi cho trẻ em có hình dạng gồm một hình lập phương có cạnh dài 1,2m và nóc lều
Đề bài
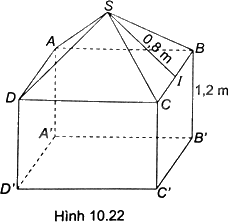
Một cái lều đồ chơi cho trẻ em có hình dạng gồm một hình lập phương có cạnh dài 1,2m và nóc lều là một hình chóp tứ giác đều có cạnh đáy bằng 1,2m, trung đoạn bằng 0,8m (H.10.22). Tính diện tích vải để phủ nóc và các mặt bên của lều (coi các mép nối không đáng kể).
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức về diện tích xung quanh của hình chóp tam giác đều để tính diện tích nóc lều: Diện tích xung quanh của hình chóp tứ giác đều bằng tích của nửa chu vi đáy với trung đoạn.
Lời giải chi tiết
Diện tích các mặt bên của lều là: \({S_1} = 4.1,{2^2} = 5,76\left( {{m^2}} \right)\)
Diện tích nóc lều là: \({S_2} = 4.\left( {\frac{1}{2}.1,2.0,8} \right) = 1,92\left( {{m^2}} \right)\)
Diện tích vải để phủ nóc và các mặt bên của lều là: \(S = {S_1} + {S_2} = 5,76 + 1,92 = 7,68\left( {{m^2}} \right)\)
Bài 10.19 trang 80 sách bài tập Toán 8 - Kết nối tri thức với cuộc sống thuộc chương trình học Toán 8, tập trung vào việc vận dụng các kiến thức về hình học, cụ thể là các tính chất của hình thang cân và cách tính diện tích hình thang. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững các khái niệm cơ bản và các công thức liên quan.
Bài 10.19 thường yêu cầu học sinh chứng minh một hình thang là hình thang cân, tính độ dài các cạnh, đường chéo hoặc diện tích của hình thang. Để giải quyết bài toán, cần:
(Giả sử bài toán yêu cầu chứng minh hình thang ABCD là hình thang cân và tính diện tích của nó, với AB = 5cm, CD = 10cm, AD = BC = 6cm, chiều cao h = 4cm)
Chứng minh ABCD là hình thang cân:
Xét tam giác ABD và tam giác BAC:
Vậy, tam giác ABD = tam giác BAC (c-g-c). Suy ra BD = AC. Do đó, ABCD là hình thang cân.
Tính diện tích hình thang ABCD:
Áp dụng công thức tính diện tích hình thang: S = (AB + CD) * h / 2 = (5 + 10) * 4 / 2 = 30 cm2
Ngoài bài 10.19, còn rất nhiều bài tập tương tự liên quan đến hình thang cân. Các bài tập này thường yêu cầu:
Để giải các bài tập này, học sinh cần nắm vững các kiến thức về hình thang cân, các tính chất của nó và các công thức liên quan. Ngoài ra, cần rèn luyện kỹ năng vẽ hình, phân tích bài toán và vận dụng các kiến thức đã học để giải quyết bài toán một cách hiệu quả.
Để củng cố kiến thức và kỹ năng giải bài tập về hình thang cân, học sinh có thể tự giải thêm các bài tập sau:
Giaitoan.edu.vn hy vọng rằng bài viết này đã cung cấp cho các em những kiến thức và kỹ năng cần thiết để giải bài 10.19 trang 80 sách bài tập Toán 8 - Kết nối tri thức với cuộc sống một cách hiệu quả. Chúc các em học tập tốt!