Bài 3.11 trang 34 sách bài tập Toán 8 thuộc chương 3: Các góc tạo bởi một đường thẳng cắt hai đường thẳng. Bài tập này yêu cầu học sinh vận dụng kiến thức về các góc so le trong, đồng vị, trong cùng phía để chứng minh tính chất của các góc.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 3.11 trang 34 sách bài tập Toán 8 - Kết nối tri thức với cuộc sống, giúp các em học sinh nắm vững kiến thức và rèn luyện kỹ năng giải bài tập.
Cho hình thang cân ABCD với hai đáy AB và CD, đường chéo AC vuông góc với cạnh bên AD
Đề bài
Cho hình thang cân ABCD với hai đáy AB và CD, đường chéo AC vuông góc với cạnh bên AD, tia CA là tia phân giác của góc C. Tính chu vi của hình thang đó biết rằng \(AD = 2cm\).
Phương pháp giải - Xem chi tiết
Sử dụng tính chất của hình thang cân, tam giác và công thức tính chu vi hình thang.
Lời giải chi tiết
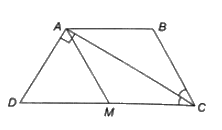
Do CA là tia phân giác của \(\widehat C\) nên \(\widehat {BCA} = \widehat {ACD}\)
Mà ABCD là hình thang cân nên \(AB//CD\), suy ra \(\widehat {BCA} = \widehat {ACD}\) hai góc so le trong)
Do đó, \(\widehat {BAC} = \widehat {BCA}\), suy ra \(\Delta ABC\) cân tại B.
Đặt \(\widehat {BAC} = \alpha \) thì \(\widehat C = 2\alpha \).
Vì ABCD là hình thang cân nên \(\widehat D = \widehat C = 2\alpha \).
Tam giác ADC vuông tại A nên \(\widehat {ADC} + \widehat {ACD} = 2\alpha + \alpha = 90^\circ \)
, suy ra \(\alpha = 30^\circ \), \(\widehat D = 60^\circ \).
Lấy điểm M thuộc cạnh huyền DC sao cho\(DM = AD\), mà \(\widehat D = 60^\circ \) thì \(\Delta AMD\)là tam giác đều, nên \(\widehat {MAD} = 60^\circ \).
Khi đó \(\widehat {MAC} = \widehat {CAD} - \widehat {MAD} = 90^\circ - 60^\circ = 30^\circ \)
Suy ra \(\widehat {ACM} = \widehat {CAM} = 30^\circ \) nên tam giác MAC cân tại M
Do đó \(AM = MC\), mà \(AM = DM = AD\)
Nên \(AM = DM = AD = MC\) hay \(DC = 2AD.\)
Vậy \(AB = BC = AD,DC = 2AD\) nên chu vi hình thang bằng
\(AB + BC + CD + AD = 5AD = 5.2 = 10cm\).
Bài 3.11 trang 34 sách bài tập Toán 8 - Kết nối tri thức với cuộc sống là một bài tập quan trọng giúp học sinh củng cố kiến thức về các góc tạo bởi một đường thẳng cắt hai đường thẳng. Để giải bài tập này, học sinh cần nắm vững các định nghĩa và tính chất của các góc so le trong, đồng vị, trong cùng phía.
Cho hình vẽ sau (hình vẽ cần được mô tả chi tiết, ví dụ: a // b và có đường thẳng c cắt a và b). Yêu cầu: Tìm các cặp góc so le trong, đồng vị, trong cùng phía.
(Phần này sẽ trình bày lời giải chi tiết của bài tập, bao gồm các bước giải, giải thích rõ ràng và chính xác. Ví dụ:)
Vì a // b và c là đường thẳng cắt a và b, ta có:
(Giải thích chi tiết hơn về cách xác định các góc này dựa trên hình vẽ.)
Để hiểu rõ hơn về cách giải bài tập này, chúng ta cùng xem xét một ví dụ khác. (Ví dụ khác cần được trình bày chi tiết, tương tự như bài tập 3.11)
Để rèn luyện thêm kỹ năng giải bài tập về các góc tạo bởi một đường thẳng cắt hai đường thẳng, các em có thể làm thêm các bài tập sau:
Bài 3.11 trang 34 sách bài tập Toán 8 - Kết nối tri thức với cuộc sống là một bài tập cơ bản nhưng quan trọng. Việc nắm vững kiến thức và phương pháp giải bài tập này sẽ giúp các em học sinh học tốt môn Toán 8. Giaitoan.edu.vn hy vọng rằng với lời giải chi tiết và dễ hiểu này, các em sẽ tự tin hơn khi giải các bài tập tương tự.
| Góc | Định nghĩa |
|---|---|
| So le trong | Là hai góc nằm bên trong hai đường thẳng song song và ở hai phía của đường thẳng cắt. |
| Đồng vị | Là hai góc nằm ở cùng phía của đường thẳng cắt và có vị trí tương ứng. |
| Trong cùng phía | Là hai góc nằm bên trong hai đường thẳng song song và ở cùng một phía của đường thẳng cắt. |