Bài 3.19 trang 37 sách bài tập Toán 8 thuộc chương trình Kết nối tri thức với cuộc sống là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng áp dụng kiến thức về các góc tạo bởi đường thẳng cắt đường thẳng. Bài tập này thường yêu cầu học sinh phải phân tích hình vẽ, xác định các góc so le trong, đồng vị, và sử dụng các tính chất của chúng để tính toán.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 3.19 trang 37 sách bài tập Toán 8, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Cho tam giác ABC không vuông tại A. Dựng bên ngoài tam giác đó hai tam giác ABD, ACE vuông cân tại đỉnh A rồi dựng hình bình hành AEID.
Đề bài
Cho tam giác ABC không vuông tại A. Dựng bên ngoài tam giác đó hai tam giác ABD, ACE vuông cân tại đỉnh A rồi dựng hình bình hành AEID.
a) Chứng minh hai tam giác ABC và DAI bằng nhau.
b) Chứng minh đường thẳng AI vuông góc với BC.
c) Chứng minh đường thẳng BE vuông góc với đường thẳng CD.
d) Gọi K là trung điểm của BD, chứng minh \(KC = KI\) và KC vuông góc với KI
(Gợi ý: Chứng minh hai tam giác AKI và BKC bằng nhau).
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức về tính chất hình bình hành để chứng minh: Hình bình hành có các cạnh đối bằng nhau và song song.
Lời giải chi tiết
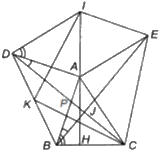
a) Vì AEID là hình bình hành nên \(\widehat {ADI} + \widehat {DAE} = {180^0}\) (hai góc kề một cạnh của hình bình hành)
Ta có: \(\widehat {DAE} + \widehat {DAB} + \widehat {BAC} + \widehat {CAE} = {360^0}\)
Mà tam giác ABD vuông tại A, tam giác ACE vuông tại A nên \(\widehat {BAC} + \widehat {DAE} = {360^0} - {90^0} - {90^0} = {180^0}\)
Do đó, \(\widehat {ADI} = \widehat {BAC}\)
Tam giác ABD vuông cân tại A nên \(AB = AD\)
Tam giác ACE vuông cân tại A nên \(AC = AE\)
Vì AEID là hình bình hành nên \(AE = DI\), do đó \(DI = AC\)
Tam giác ADI và tam giác BAC có:
\(AB = AD\)(cmt), \(\widehat {ADI} = \widehat {BAC}\) (cmt), \(DI = AC\) (cmt)
Do đó, \(\Delta ADI = \Delta BAC\left( {c - g - c} \right)\)
b) Giả sử AI cắt BC ở H.
Ta có: \(\widehat {DAI} + \widehat {DAB} + \widehat {BAH} = {180^0}\), mà \(\widehat {DAB} = {90^0}\) (do tam giác DAB vuông cân tại A). Suy ra \(\widehat {DAI} + \widehat {BAH} = {90^0}\)
Mà \(\widehat {DAI} = \widehat {ABC}\) (do \(\Delta ADI = \Delta BAC\)) nên \(\widehat {ABH} + \widehat {BAH} = {90^0}\)
Tam giác ABH có: \(\widehat {ABH} + \widehat {BAH} + \widehat {AHB} = {180^0}\) nên \(\widehat {AHB} = {180^0} - \left( {\widehat {ABH} + \widehat {BAH}} \right) = {90^0}\)
Do đó, AI vuông góc với BC tại H.
c) Ta có: \(\widehat {BAE} = \widehat {BAC} + \widehat {CAE} = \widehat {BAC} + {90^0}\)
\(\widehat {DAC} = \widehat {BAC} + \widehat {BAD} = \widehat {BAC} + {90^0}\)
Do đó, \(\widehat {BAE} = \widehat {DAC}\)
Tam giác BAE và tam giác DAC có:
\(AB = AD\left( {cmt} \right),\widehat {BAE} = \widehat {DAC}\left( {cmt} \right),AE = AC\left( {cmt} \right)\)
Do đó, \(\Delta BAE = \Delta DAC\left( {c - g - c} \right)\), suy ra \(\widehat {EBA} = \widehat {CDA}\)
Gọi J là giao điểm của DC và BE, ta có: \(\widehat {JBA} = \widehat {JDA}\)
Gọi P là giao điểm của AB và CD.
Tam giác ADP vuông tại A nên \(\widehat {PDA} + \widehat {DPA} = {90^0}\)
Mà \(\widehat {PDA} = \widehat {JBP},\widehat {DPA} = \widehat {BPJ}\) (đối đỉnh)
Do đó, \(\widehat {JBP} + \widehat {BPJ} = {90^0}\), suy ra \(\widehat {BJP} = {90^0}\) hay BE vuông góc với đường thẳng CD.
d) Tam giác ABD vuông cân tại A nên AK vừa là đường trung tuyến, vừa là đường cao, đường phân giác. Do đó, \(\widehat {DAK} = \frac{1}{2}\widehat {BAD} = {45^0}\)
Khi đó, \(\widehat {ABK} = \widehat {BAK} = {45^0}\) nên tam giác ABK vuông cân tại K, do đó, \(KA = KB\)
Ta có: \(\widehat {KAI} = \widehat {DAK} + \widehat {DAI} = {45^0} + \widehat {DAI} = {45^0} + \widehat {ABC}\)
Mặt khác \(\widehat {KBC} = \widehat {ABK} + \widehat {ABC} = {45^0} + \widehat {ABC}\)
Do đó, \(\widehat {KAI} = \widehat {KBC}\)
Tam giác AKI và tam giác BKC có:
\(AK = BK,\widehat {KAI} = \widehat {KBC},AI = BC\) (do \(\Delta ADI = \Delta BAC\))
Suy ra \(\Delta AKI = \Delta BKC\left( {c - g - c} \right)\) nên \(KI = KC\); \(\widehat {AKI} = \widehat {BKC}\)
Ta có: \(\widehat {AKC} + \widehat {BKC} = {90^0}\), mà \(\widehat {AKI} = \widehat {BKC}\) nên \(\widehat {AKC} + \widehat {AKI} = {90^0}\) hay \(\widehat {IKC} = {90^0}\) nên KC vuông góc với KI.
Bài 3.19 trang 37 sách bài tập Toán 8 - Kết nối tri thức với cuộc sống yêu cầu học sinh vận dụng kiến thức về các góc tạo bởi đường thẳng cắt đường thẳng để giải quyết các bài toán thực tế. Dưới đây là hướng dẫn chi tiết cách giải bài tập này:
Trước khi bắt đầu giải bài tập, học sinh cần đọc kỹ đề bài để hiểu rõ yêu cầu. Xác định các yếu tố quan trọng trong đề bài như hình vẽ, các góc đã cho, và yêu cầu tính toán.
Để giải bài 3.19, học sinh cần nắm vững các kiến thức sau:
(Nội dung lời giải chi tiết bài 3.19 sẽ được trình bày tại đây, bao gồm hình vẽ minh họa, các bước giải, và giải thích rõ ràng từng bước. Ví dụ:)
Đề bài: Cho hình vẽ, biết góc A1 = 60 độ. Tính các góc còn lại.
Giải:
Vậy, góc A3 = 60 độ, góc A2 = 120 độ, và góc A4 = 120 độ.
Ngoài bài 3.19, còn rất nhiều bài tập tương tự yêu cầu học sinh vận dụng kiến thức về các góc tạo bởi đường thẳng cắt đường thẳng. Để giải các bài tập này, học sinh có thể áp dụng các phương pháp sau:
Để nắm vững kiến thức về các góc tạo bởi đường thẳng cắt đường thẳng, học sinh nên luyện tập thêm các bài tập khác trong sách bài tập và các tài liệu tham khảo. Việc luyện tập thường xuyên sẽ giúp học sinh hiểu sâu hơn về kiến thức và rèn luyện kỹ năng giải bài tập.
Bài 3.19 trang 37 sách bài tập Toán 8 - Kết nối tri thức với cuộc sống là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng áp dụng kiến thức về các góc tạo bởi đường thẳng cắt đường thẳng. Hy vọng với hướng dẫn chi tiết trên, các em học sinh sẽ tự tin giải bài tập này và các bài tập tương tự.
| Góc | Giá trị |
|---|---|
| A1 | 60 độ |
| A2 | 120 độ |
| A3 | 60 độ |
| A4 | 120 độ |