Bài 3.9 trang 34 sách bài tập Toán 8 - Kết nối tri thức với cuộc sống là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng áp dụng các kiến thức về hình học đã học vào giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 3.9 này, giúp các em học sinh nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Cho tam giác ABC vuông cân tại đỉnh A. Ghép thêm vào phía ngoài tam giác đó tam giác BCD vuông cân tại đỉnh B.
Đề bài
Cho tam giác ABC vuông cân tại đỉnh A. Ghép thêm vào phía ngoài tam giác đó tam giác BCD vuông cân tại đỉnh B. Chứng minh tứ giác ABDC là một hình thang vuông (hình thang có một cạnh bên vuông góc với đáy).
Phương pháp giải - Xem chi tiết
Sử dụng tính chất của tam giác cân, tổng ba góc của tam giác; dấu hiệu nhận biết hình thang, hình thang vuông.
Lời giải chi tiết
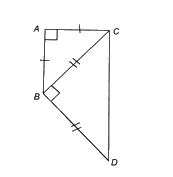
Do \(\Delta ABC\) vuông cân tại đỉnh A nên \(\widehat {ABC} = \widehat {ACB}\); \(\widehat A = 90^\circ \)
Xét trong \(\Delta ABC\) có \(\widehat {ABC} + \widehat {ACB} + \widehat A = 180^\circ \)
Nên \(\widehat {ABC} = \widehat {ACB} = \frac{{180^\circ - \widehat A}}{2} = \frac{{180^\circ - 90^\circ }}{2} = 45^\circ \)
Tương tự do \(\Delta BCD\) vuông cân tại đỉnh B nên \(\widehat {BCD} = \widehat {BDC}\); \(\widehat {CBD} = 90^\circ \)
Xét trong \(\Delta BCD\) có \(\widehat {BCD} + \widehat {BDC} + \widehat {CBD} = 180^\circ \)
Nên \(\widehat {BCD} = \widehat {BDC} = \frac{{180^\circ - \widehat {CBD}}}{2} = \frac{{180^\circ - 90^\circ }}{2} = 45^\circ \).
Ta có \(\widehat {ABC} = 45^\circ = \widehat {BCD}\) nên AB // CD (hai góc so le trong bằng nhau).
Vậy ABCD là một hình thang với AB, CD là hai đáy; cạnh bên của hình thang là AC vuông góc với đáy AB nên hình thang đó là hình thang vuông.
Bài 3.9 yêu cầu chúng ta xét hình thang cân ABCD (AB // CD, AD = BC) và tìm mối quan hệ giữa các góc. Để giải bài này, chúng ta cần nắm vững các tính chất của hình thang cân, đặc biệt là tính chất về các góc kề một cạnh bên và tổng hai góc kề một đáy.
Đề bài: Cho hình thang cân ABCD (AB // CD, AD = BC). Tính số đo các góc của hình thang cân đó, biết rằng ∠A = 80°.
Giải:
Bài toán này giúp chúng ta hiểu rõ hơn về mối liên hệ giữa các góc trong hình thang cân. Việc nắm vững các tính chất của hình thang cân là rất quan trọng để giải quyết các bài toán liên quan đến hình học. Ngoài ra, chúng ta có thể mở rộng bài toán bằng cách xét các trường hợp khác nhau của góc A, ví dụ như ∠A = 90°, ∠A > 90° để tìm hiểu thêm về các góc còn lại của hình thang cân.
Xét hình thang cân MNPQ (MN // PQ, MP = NQ). Nếu ∠M = 110°, hãy tính số đo các góc còn lại của hình thang cân đó.
Giải:
Để củng cố kiến thức về hình thang cân và các tính chất của nó, các em có thể tự giải thêm các bài tập sau:
Bài 3.9 trang 34 sách bài tập Toán 8 - Kết nối tri thức với cuộc sống là một bài tập cơ bản nhưng quan trọng trong chương trình học Toán 8. Hy vọng với lời giải chi tiết và các phân tích trên, các em học sinh sẽ hiểu rõ hơn về bài toán này và tự tin hơn trong quá trình học tập. Chúc các em học tốt!