Bài 8.14 trang 45 sách bài tập Toán 8 - Kết nối tri thức là một bài tập quan trọng trong chương trình học Toán 8. Bài tập này yêu cầu học sinh vận dụng kiến thức đã học về hình học để giải quyết các vấn đề thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 8.14 trang 45, giúp các em học sinh hiểu rõ bản chất bài toán và tự tin làm bài tập.
Số liệu thống kê về 1 830 vụ tai nạn giao thông ở một thành phố cho trong bảng sau:
Đề bài
Số liệu thống kê về 1 830 vụ tai nạn giao thông ở một thành phố cho trong bảng sau:
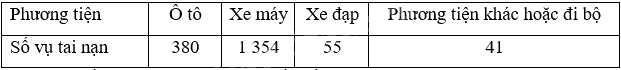
Tính xác suất thực nghiệm của các biến cố sau:
a) E: “Gặp tai nạn khi đi ô tô”;
b) F: “Gặp tai nạn khi đi xe máy hoặc xe đạp”;
c) G: “Gặp tai nạn khi đi xe đạp, phương tiện khác hoặc đi bộ ”.
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức xác suất thực nghiệm của một biến cố để tính: Giả sử trong n lần thực nghiệm hoặc n lần theo dõi (quan sát) một hiện tượng ta thấy biến cố E xảy ra k lần. Khi đó xác suất thực nghiệm của biến cố E bằng \(\frac{k}{n}\), tức là bằng tỉ số giữa số lần xuất hiện biến cố E và số lần thực hiện thực nghiệm hoặc theo dõi hiện tượng đó.
Lời giải chi tiết
a) Có 380 vụ tai nạn khi đi ô tô, do đó xác suất thực nghiệm của biến cố E là: \(\frac{{380}}{{1\;830}} = \frac{{38}}{{183}}\)
b) Số vụ tai nạn khi đi xe máy hoặc xe đạp là: \(1\;354 + 55 = 1\;409\) nên xác suất thực nghiệm của biến cố F là: \(\frac{{1\;409}}{{1\;830}}\)
c) Số vụ tai nạn khi đi xe đạp, phương tiện khác hoặc đi bộ là: \(55 + 41 = 96\) nên xác suất thực nghiệm của biến cố G là: \(\frac{{96}}{{1\;830}} = \frac{{16}}{{305}}\)
Bài 8.14 trang 45 sách bài tập Toán 8 - Kết nối tri thức yêu cầu chúng ta giải quyết một bài toán liên quan đến hình học, cụ thể là việc chứng minh các tính chất của hình thang cân. Để giải bài toán này một cách hiệu quả, chúng ta cần nắm vững các kiến thức cơ bản về hình thang cân, bao gồm:
Đề bài: Cho hình thang cân ABCD (AB // CD). Gọi E là giao điểm của AD và BC. Chứng minh rằng:
Lời giải:
a) Chứng minh EA = EB:
Xét tam giác ADE và tam giác BCE:
Do đó, tam giác ADE đồng dạng với tam giác BCE (g-g). Suy ra:
EA/EB = AD/BC = 1 (vì AD = BC)
Vậy EA = EB.
b) Chứng minh EC = ED:
Xét tam giác EDC:
∠EDC = ∠ECD (do tam giác ADE đồng dạng với tam giác BCE)
Suy ra tam giác EDC là tam giác cân tại E.
Vậy EC = ED.
Ngoài bài 8.14, còn rất nhiều bài tập tương tự liên quan đến hình thang cân. Để giải quyết các bài tập này, bạn cần:
Một số dạng bài tập thường gặp:
Để củng cố kiến thức và kỹ năng giải bài tập về hình thang cân, bạn có thể luyện tập thêm các bài tập sau:
Bài 8.14 trang 45 sách bài tập Toán 8 - Kết nối tri thức là một bài tập quan trọng giúp học sinh hiểu rõ hơn về hình thang cân và các tính chất của nó. Hy vọng với lời giải chi tiết và hướng dẫn giải bài tập trên, các em học sinh sẽ tự tin hơn trong việc học Toán 8.
Giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán. Chúc các em học tập tốt!