Bài 7.46 trang 36 sách bài tập Toán 8 - Kết nối tri thức là một bài tập quan trọng trong chương trình học Toán 8. Bài tập này yêu cầu học sinh vận dụng kiến thức đã học về các định lý, tính chất của hình học để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 7.46 trang 36 sách bài tập Toán 8 - Kết nối tri thức, giúp các em học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
Cho hàm số \(y = \left( {2m - 1} \right)x + 5\left( {m \ne \frac{1}{2}} \right)\)
Đề bài
Cho hàm số \(y = \left( {2m - 1} \right)x + 5\left( {m \ne \frac{1}{2}} \right)\)
a) Tìm m để đồ thị hàm số song song với đường thẳng \(y = - 3x\)
b) Vẽ đồ thị hàm số với giá trị m vừa tìm được ở câu a.
c) Tìm giao điểm A của đồ thị hàm số ở câu b và đồ thị của hàm số \(y = x + 5\). Tính diện tích của tam giác OAB, trong đó B là giao điểm của đồ thị hàm số \(y = x + 5\) với trục Ox.
Phương pháp giải - Xem chi tiết
a) Sử dụng kiến thức vị trí tương đối của hai đường thẳng để tìm m:
Cho hai đường thẳng \(\left( d \right):y = ax + b\left( {a \ne 0} \right)\,\) và \(\left( {d'} \right):y = a'x + b'\left( {a' \ne 0} \right)\,\). Khi đó, d song song với d’ nếu \(a = a',b \ne b'\)
b) Sử dụng kiến thức về cách vẽ đồ thị hàm số bậc nhất \(y = ax + b\left( {a \ne 0} \right)\) để vẽ đồ thị:
+ Khi \(b = 0\) thì \(y = ax\). Đồ thị của hàm số \(y = ax\) là đường thẳng đi qua gốc tọa độ O(0; 0) và điểm A(1; a)
+ Khi \(b \ne 0\), ta thường xác định hai điểm đặc biệt trên đồ thị là giao điểm của đồ thị với hai trục tọa độ như sau:
- Cho \(x = 0\) thì \(y = b\), ta được điểm P(0; b) thuộc trục tung Oy.
- Cho \(y = 0\) thì \(x = \frac{{ - b}}{a}\), ta được điểm \(Q\left( { - \frac{b}{a};0} \right)\) thuộc trục hoành Ox.
- Vẽ đường thẳng đi qua hai điểm P, Q ta được đồ thị của hàm số \(y = ax + b\)
c) + Tìm tọa độ giao điểm của hai đường thẳng theo các bước:
Bước 1: Xét phương trình hoành độ giao điểm của hai đường thẳng đó để tìm hoành độ giao điểm.
Bước 2: Thay hoành độ giao điểm vừa tìm được vào một trong hai hàm số ta tìm được tung độ giao điểm.
+ Tam giác OAB vuông tại O nên diện tích tam giác AOB là: \(S = \frac{1}{2}OA.OB\)
Lời giải chi tiết
a) Vì đồ thị hàm số \(y = \left( {2m - 1} \right)x + 5\) song song với đường thẳng \(y = - 3x\) nên \(2m - 1 = - 3\)
\(2m = - 2\), suy ra\(m = - 1\) (thỏa mãn)
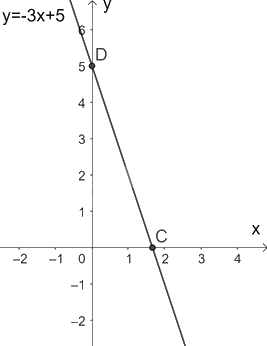
b) Với \(m = - 1\) ta có: \(y = - 3x + 5\)
Đồ thị hàm số \(y = - 3x + 5\) đi qua hai điểm \(D\left( {0;5} \right),C\left( {\frac{5}{3};0} \right)\)
c) Hoành độ giao điểm của hai đồ thị hàm số \(y = x + 5\) và \(y = - 3x + 5\) là nghiệm của phương trình: \(x + 5 = - 3x + 5\)
\(x = 0\) nên \(y = 5\)
Do đó, điểm \(A\left( {0;5} \right)\)
Vì B là giao điểm của đồ thị hàm số \(y = x + 5\) với trục Ox nên \(x + 5 = 0\), suy ra \(x = - 5\)
Do đó, \(B\left( { - 5;0} \right)\)
Vì tam giác OAB vuông tại O nên diện tích tam giác OAB là: \(\frac{1}{2}OA.OB = \frac{1}{2}.5.\left| { - 5} \right| = \frac{{25}}{2}\)
Bài 7.46 trang 36 sách bài tập Toán 8 - Kết nối tri thức yêu cầu học sinh chứng minh một tính chất liên quan đến đường trung bình của tam giác. Để giải bài này, chúng ta cần nắm vững định nghĩa và các tính chất của đường trung bình trong tam giác.
Cho tam giác ABC. Gọi D, E, F lần lượt là trung điểm của BC, CA, AB. Chứng minh rằng tam giác DEF đồng dạng với tam giác ABC.
Để chứng minh hai tam giác đồng dạng, chúng ta có thể sử dụng một trong các trường hợp đồng dạng tam giác: góc - góc (g-g), cạnh - cạnh - cạnh (c-c-c), hoặc cạnh - góc - cạnh (c-g-c). Trong bài toán này, việc chứng minh các cạnh tương ứng tỉ lệ là một hướng đi hợp lý.
Vì D là trung điểm của BC và E là trung điểm của AC, nên DE là đường trung bình của tam giác ABC. Do đó, DE song song với AB và DE = 1/2 AB.
Vì E là trung điểm của AC và F là trung điểm của AB, nên EF là đường trung bình của tam giác ABC. Do đó, EF song song với BC và EF = 1/2 BC.
Vì F là trung điểm của AB và D là trung điểm của BC, nên FD là đường trung bình của tam giác ABC. Do đó, FD song song với AC và FD = 1/2 AC.
Từ các kết quả trên, ta có:
Suy ra DE/AB = EF/BC = FD/AC = 1/2. Do đó, tam giác DEF đồng dạng với tam giác ABC theo trường hợp cạnh - cạnh - cạnh (c-c-c).
Bài toán này là một ứng dụng quan trọng của định lý về đường trung bình của tam giác. Việc hiểu rõ và vận dụng linh hoạt định lý này sẽ giúp học sinh giải quyết nhiều bài toán hình học khác một cách dễ dàng.
Ngoài ra, bài toán còn giúp học sinh rèn luyện kỹ năng chứng minh hình học, tư duy logic và khả năng phân tích vấn đề.
Để củng cố kiến thức về đường trung bình của tam giác, các em có thể tự giải các bài tập sau:
Hy vọng với lời giải chi tiết và dễ hiểu trên, các em học sinh đã nắm vững phương pháp giải bài 7.46 trang 36 sách bài tập Toán 8 - Kết nối tri thức. Chúc các em học tập tốt và đạt kết quả cao trong môn Toán!
Giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục kiến thức Toán học.