Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho bài 13 trang 82 sách bài tập Toán 8 Kết nối tri thức. Bài viết này sẽ giúp bạn nắm vững kiến thức, rèn luyện kỹ năng giải toán và đạt kết quả tốt nhất trong môn Toán.
Chúng tôi hiểu rằng việc tự học Toán đôi khi gặp nhiều khó khăn. Vì vậy, đội ngũ giáo viên giàu kinh nghiệm của giaitoan.edu.vn đã biên soạn lời giải bài 13 trang 82 một cách cẩn thận, đảm bảo tính chính xác và dễ tiếp thu.
Cho tam giác ABC có \(AB = 3cm,AC = 4cm,BC = 5cm.\) Lấy điểm D trên cạnh BC sao cho \(BD = 2cm.\)
Đề bài
Cho tam giác ABC có \(AB = 3cm,AC = 4cm,BC = 5cm.\) Lấy điểm D trên cạnh BC sao cho \(BD = 2cm.\) Lấy các điểm E, F trên các cạnh AB, AC sao cho DE, DF lần lượt vuông góc với AB, AC.
a) Chứng minh rằng $\Delta BDE\backsim \Delta DCF$
b) Tính độ dài đoạn thẳng AD.
Phương pháp giải - Xem chi tiết
a) + Sử dụng kiến thức về định lý Pythagore đảo để chứng minh tam giác ABC vuông tại A: Nếu một tam giác có bình phương của một cạnh bằng tổng các bình phương của hai cạnh kia thì tam giác đó là tam giác vuông.
+ Sử dụng kiến thức về định lý (trường hợp đồng dạng góc – góc) để chứng minh: Nếu hai góc của tam giác lần lượt bằng hai góc của tam giác kia thì hai tam giác đó đồng dạng với nhau.
b) Sử dụng kiến thức định lí Pythagore để tính AD: Trong một tam giác vuông, bình phương cạnh huyền bằng tổng các bình phương của hai cạnh góc vuông.
Lời giải chi tiết
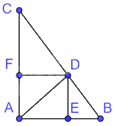
a) Tam giác ABC có: \(A{B^2} + A{C^2} = B{C^2}\left( {do\;{3^2} + {4^2} = {5^2}} \right)\) nên tam giác ABC vuông tại A (định lí Pythagore đảo). Do đó, \(\widehat {BAC} = {90^0}\)
Vì DE, DF lần lượt vuông góc với AB, AC nên\(DE \bot AB,DF \bot AC\)
Do đó, \(\widehat {DFC} = \widehat {DFA} = \widehat {DEA} = \widehat {DEB} = {90^0}\)
Tứ giác AEDF có: \(\widehat {DFA} = \widehat {DEA} = \widehat {FAE} = {90^0}\) nên tứ giác AEDF là hình chữ nhật. Do đó, \(\widehat {FDE} = {90^0}\)
Mà \(\widehat {CDF} + \widehat {FDE} + \widehat {EDB} = {180^0}\) nên \(\widehat {CDF} + \widehat {EDB} = {90^0}\)
Tam giác BDE và tam giác DCF có:
\(\widehat {DEB} = \widehat {DFC} = {90^0},\widehat B = \widehat {FDC}\left( { = {{90}^0} - \widehat {EDB}} \right)\)
Do đó, $\Delta BDE\backsim \Delta DCF\left( g-g \right)$
b) Tam giác ABC có: DE//AC (cùng vuông góc với AB) nên $\Delta BDE\backsim \Delta BCA$, do đó \(\frac{{BD}}{{BC}} = \frac{{ED}}{{AC}} = \frac{{EB}}{{AB}}\). Suy ra: \(\frac{{DE}}{4} = \frac{{EB}}{3} = \frac{2}{5}\)
Do đó: \(DE = \frac{8}{5}cm,EB = \frac{6}{5}cm \Rightarrow EA = \frac{9}{5}cm\)
Áp dụng định lí Pythagore vào tam giác AED vuông tại E có: \(A{D^2} = A{E^2} + E{D^2} = {\left( {\frac{9}{5}} \right)^2} + {\left( {\frac{8}{5}} \right)^2} = \frac{{29}}{5}\) nên \(AD = \sqrt {\frac{{29}}{5}} cm\)
Bài 13 trang 82 sách bài tập Toán 8 Kết nối tri thức thuộc chương trình học Toán 8, tập trung vào việc vận dụng các kiến thức về hình học, cụ thể là các tính chất của hình thang cân. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững các khái niệm cơ bản như:
Trước khi bắt tay vào giải bài tập, hãy đọc kỹ đề bài và xác định rõ yêu cầu. Thông thường, bài tập về hình thang cân sẽ yêu cầu tính độ dài các cạnh, góc, đường cao hoặc chứng minh một tính chất nào đó. Phương pháp giải thường được sử dụng là:
(Ở đây sẽ là nội dung giải chi tiết từng phần của bài 13, bao gồm các bước giải, giải thích rõ ràng và minh họa bằng hình vẽ nếu cần thiết. Nội dung này sẽ được trình bày chi tiết và đầy đủ, đảm bảo học sinh có thể hiểu và tự giải được các bài tập tương tự.)
Bài toán: Cho hình thang cân ABCD (AB // CD), AB = 10cm, CD = 20cm, AD = BC = 13cm. Tính chiều cao của hình thang.
Giải:
Kẻ AH và BK vuông góc với CD (H, K thuộc CD). Khi đó, AH = BK là chiều cao của hình thang.
Vì ABCD là hình thang cân nên DH = KC = (CD - AB) / 2 = (20 - 10) / 2 = 5cm.
Xét tam giác vuông ADH, ta có: AH2 = AD2 - DH2 = 132 - 52 = 169 - 25 = 144.
Suy ra, AH = √144 = 12cm.
Vậy, chiều cao của hình thang ABCD là 12cm.
Để củng cố kiến thức và rèn luyện kỹ năng giải toán, bạn có thể tham khảo thêm các bài tập tương tự trong sách bài tập Toán 8 Kết nối tri thức hoặc trên các trang web học toán online khác. Việc luyện tập thường xuyên sẽ giúp bạn tự tin hơn khi đối mặt với các bài toán khó.
Bài 13 trang 82 sách bài tập Toán 8 Kết nối tri thức là một bài tập quan trọng giúp học sinh hiểu sâu hơn về hình thang cân và các tính chất của nó. Hy vọng rằng, với lời giải chi tiết và hướng dẫn cụ thể trong bài viết này, bạn sẽ giải bài tập một cách dễ dàng và hiệu quả. Chúc bạn học tốt!