Bài 6.5 trang 4 sách bài tập Toán 8 Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng áp dụng kiến thức về các phép biến đổi đại số. Bài tập này thường yêu cầu học sinh phải thực hiện các phép tính, rút gọn biểu thức hoặc chứng minh đẳng thức.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 6.5 trang 4 sách bài tập Toán 8 Kết nối tri thức, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Tìm tập hợp các giá trị nguyên của x sao cho \(P\left( x \right) = \frac{2}{{x + 1}}\) có giá trị là số nguyên.
Đề bài
Tìm tập hợp các giá trị nguyên của x sao cho \(P\left( x \right) = \frac{2}{{x + 1}}\) có giá trị là số nguyên.
Phương pháp giải - Xem chi tiết
+ Sử dụng kiến thức giá trị của phân thức tại một giá trị đã cho của biến để tính giá trị phân thức: Muốn tính giá trị của một phân thức tại một giá trị đã cho của biến ta thay giá trị đã cho của biến vào phân thức đó rồi tính giá trị biểu thức số nhận được.
+ Một phân số là số nguyên khi tử số chia hết cho mẫu số (hay mẫu số là ước của tử số).
Lời giải chi tiết
Điều kiện xác định \(x \ne - 1\)
Để P(x) có giá trị là một số nguyên thì \(\left( {x + 1} \right) \in \) Ư(2)\( = \left\{ {1; - 1;2; - 2} \right\}\).
Ta có bảng:
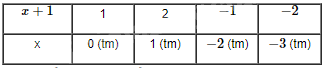
Vậy \(x \in \left\{ {0;\;1;\; - 2;\; - 3} \right\}\)
Bài 6.5 trang 4 sách bài tập Toán 8 Kết nối tri thức yêu cầu học sinh thực hiện phép nhân đa thức. Để giải bài tập này, chúng ta cần nắm vững các quy tắc nhân đa thức, bao gồm quy tắc nhân đơn thức với đa thức và quy tắc nhân đa thức với đa thức.
Bài tập 6.5 yêu cầu thực hiện các phép nhân sau:
Để nhân hai đa thức (x + 3) và (x - 2), ta áp dụng quy tắc nhân đa thức với đa thức:
(x + 3)(x - 2) = x(x - 2) + 3(x - 2) = x2 - 2x + 3x - 6 = x2 + x - 6
Tương tự, để nhân hai đa thức (2x - 1) và (x + 5), ta thực hiện:
(2x - 1)(x + 5) = 2x(x + 5) - 1(x + 5) = 2x2 + 10x - x - 5 = 2x2 + 9x - 5
Để nhân đa thức (x2 - 2x + 1) với đa thức (x + 1), ta thực hiện:
(x2 - 2x + 1)(x + 1) = x2(x + 1) - 2x(x + 1) + 1(x + 1) = x3 + x2 - 2x2 - 2x + x + 1 = x3 - x2 - x + 1
Để hiểu rõ hơn về cách nhân đa thức, chúng ta cùng xem xét một ví dụ khác:
(3x + 2)(x - 4) = 3x(x - 4) + 2(x - 4) = 3x2 - 12x + 2x - 8 = 3x2 - 10x - 8
Để củng cố kiến thức về phép nhân đa thức, các em có thể tự giải các bài tập sau:
Bài 6.5 trang 4 sách bài tập Toán 8 Kết nối tri thức là một bài tập cơ bản về phép nhân đa thức. Việc nắm vững các quy tắc nhân đa thức và thực hành thường xuyên sẽ giúp các em học sinh giải quyết các bài tập tương tự một cách dễ dàng và hiệu quả. Hy vọng với hướng dẫn chi tiết này, các em sẽ tự tin hơn trong việc học toán.
| Bài tập | Đáp án |
|---|---|
| (x - 1)(x + 1) | x2 - 1 |
| (2x + 3)(x - 2) | 2x2 - x - 6 |
| (x2 + x + 1)(x - 1) | x3 - 1 |