Bài 9.25 trang 56 sách bài tập Toán 8 - Kết nối tri thức là một bài tập quan trọng trong chương trình học Toán 8. Bài tập này yêu cầu học sinh vận dụng kiến thức về hình học, cụ thể là các tính chất của hình thang cân để giải quyết các vấn đề thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 9.25 trang 56, giúp các em học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
Cho hình thang ABCD (AB//CD). Biết rằng AD cắt BC tại E, AC cắt BD tại F.
Đề bài
Cho hình thang ABCD (AB//CD). Biết rằng AD cắt BC tại E, AC cắt BD tại F.
a) Chứng minh rằng: $\Delta EAB\backsim \Delta EDC,\Delta FAB\backsim \Delta FCD$.
b) Lấy hai điểm M, N lần lượt là trung điểm của AB, CD. Chứng minh rằng bốn điểm M, N, E, F thẳng hàng.
Phương pháp giải - Xem chi tiết
a) + Sử dụng kiến thức định lí (một trường hợp đặc biệt của hai tam giác đồng dạng) để chứng minh $\Delta EAB\backsim \Delta EDC$: Nếu một đường thẳng cắt hai cạnh của một tam giác và song song với cạnh còn lại thì nó tạo thành một tam giác mới đồng dạng với tam giác đã cho.
+ Sử dụng kiến thức về định lý (trường hợp đồng dạng góc – góc) để chứng minh $\Delta FAB\backsim \Delta FCD$: Nếu hai góc của tam giác lần lượt bằng hai góc của tam giác kia thì hai tam giác đó đồng dạng với nhau.
+ Sử dụng kiến thức về định lý (trường hợp đồng dạng góc – góc): Nếu hai góc của tam giác lần lượt bằng hai góc của tam giác kia thì hai tam giác đó đồng dạng với nhau.
b) Để chứng minh 4 điểm M, N, E, F thẳng hàng ta chứng minh:
+ Tia EM trùng với tia EN hay 3 điểm M, E, N thẳng hàng.
+ Tia FM và tia FN là hai tia đối nhau hay F, M, N thẳng hàng.
Lời giải chi tiết
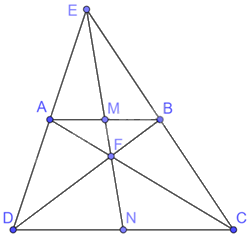
a) Tam giác EDC có: AB//CD nên $\Delta EAB\backsim \Delta EDC$
Vì AB//CD nên \(\widehat {BAC} = \widehat {ACD}\) hay \(\widehat {FAB} = \widehat {FCD}\)
Tam giác FAB và tam giác FCD có:
\(\widehat {BFA} = \widehat {CFD}\) (hai góc đối đỉnh), \(\widehat {FAB} = \widehat {FCD}\) (cmt)
Do đó, $\Delta FAB\backsim \Delta FCD\left( g-g \right)$
b) Vì $\Delta EAB\backsim \Delta EDC$(cmt) nên \(\frac{{EA}}{{ED}} = \frac{{AB}}{{DC}} = \frac{{AM}}{{DN}}\)
Tam giác EAM và tam giác EDN có:
\(\frac{{EA}}{{ED}} = \frac{{AM}}{{DN}}\) (cmt), \(\widehat {EAM} = \widehat {EDN}\) (AM//DN, hai góc đồng vị). Do đó, $\Delta EAM\backsim \Delta EDN\left( c-g-c \right)$
Suy ra: \(\widehat {AEM} = \widehat {DEN}\). Do đó, tia EM trùng với tia EN hay 3 điểm M, E, N thẳng hàng (1).
Vì nên \(\frac{{FA}}{{FC}} = \frac{{AB}}{{CD}} = \frac{{AM}}{{CN}}\)
Hai tam giác FAM và tam giác FCN có:
\(\frac{{FA}}{{FC}} = \frac{{AM}}{{CN}}\left( {cmt} \right)\), \(\widehat {FAM} = \widehat {FCN}\) (AM//CN, hai góc so le trong). Do đó, $\Delta FAM\backsim \Delta FCN\left( c-g-c \right)$ nên \(\widehat {AFM} = \widehat {CFN}\). Do đó, tia FM và tia FN là hai tia đối nhau. Suy ra, F, M, N thẳng hàng (2).
Từ (1) và (2) ta có: 4 điểm M, N, E, F thẳng hàng
Bài 9.25 trang 56 sách bài tập Toán 8 - Kết nối tri thức yêu cầu chúng ta giải quyết một bài toán liên quan đến hình thang cân. Để giải bài toán này một cách hiệu quả, chúng ta cần nắm vững các kiến thức cơ bản về hình thang cân, bao gồm:
Đề bài: (Giả sử đề bài cụ thể của bài 9.25 được đưa ra ở đây. Ví dụ: Cho hình thang cân ABCD có AB // CD, AD = BC. Gọi E là giao điểm của AC và BD. Chứng minh rằng AE = BE.)
Lời giải:
Xét tam giác ADC và tam giác BCD:
Do đó, tam giác ADC bằng tam giác BCD (c-g-c).
Suy ra AE = BE (hai cạnh tương ứng).
Các dạng bài tập tương tự:
Mẹo giải bài tập hình thang cân:
Luyện tập thêm:
Để củng cố kiến thức về hình thang cân và rèn luyện kỹ năng giải bài tập, các em học sinh có thể tham khảo thêm các bài tập sau:
Giaitoan.edu.vn hy vọng rằng với lời giải chi tiết và hướng dẫn cụ thể này, các em học sinh sẽ hiểu rõ hơn về bài 9.25 trang 56 sách bài tập Toán 8 - Kết nối tri thức và tự tin giải các bài tập tương tự. Chúc các em học tập tốt!
| Thông tin | Giá trị |
|---|---|
| Hình thang | ABCD |
| Cạnh đáy lớn | CD |
| Cạnh đáy nhỏ | AB |
| Cạnh bên | AD = BC |