Bài 10.15 trang 77 sách bài tập Toán 8 - Kết Nối Tri Thức là một bài tập quan trọng trong chương trình học Toán 8. Bài tập này yêu cầu học sinh vận dụng kiến thức đã học về các định lý, tính chất của hình học để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 10.15 trang 77, giúp các em học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
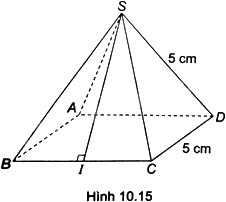
Tính diện tích xung quanh của hình chóp tứ giác đều S.ABCD trong Hình 10.15. Biết $\sqrt{18,75}\approx 4,3$
Đề bài
Tính diện tích xung quanh của hình chóp tứ giác đều S.ABCD trong Hình 10.15. Biết $\sqrt{18,75}\approx 4,3$
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức về diện tích xung quanh của hình chóp tứ giác đều để tính diện tích xung quanh hình chóp: Diện tích xung quanh của hình chóp tứ giác đều bằng tích của nửa chu vi đáy với trung đoạn.
Lời giải chi tiết
Ta có: $IB=IC=\frac{BC}{2}=2,5\left( cm \right)$
Áp dụng định lí Pythagore vào tam giác SIC vuông tại I ta có: $S{{I}^{2}}+I{{C}^{2}}=S{{C}^{2}}$
$S{{I}^{2}}={{5}^{2}}-2,{{5}^{2}}=18,75$ nên $SI=\sqrt{18,75}\approx 4,3cm$
Diện tích xung quanh của hình chóp là: ${{S}_{xq}}\approx \frac{1}{2}.4.5.4,3=43\left( c{{m}^{2}} \right)$
Bài 10.15 trang 77 sách bài tập Toán 8 - Kết Nối Tri Thức yêu cầu chúng ta giải quyết một bài toán liên quan đến hình học, cụ thể là việc chứng minh các tính chất của hình thang cân. Để giải bài toán này một cách hiệu quả, chúng ta cần nắm vững các kiến thức cơ bản về hình thang cân, bao gồm:
Đề bài: (Giả sử đề bài là: Cho hình thang cân ABCD (AB // CD). Gọi E là giao điểm của AC và BD. Chứng minh rằng EA = EB.)
Lời giải:
Kết luận: Chúng ta đã chứng minh được EA = EB, hoàn thành lời giải bài 10.15 trang 77 sách bài tập Toán 8 - Kết Nối Tri Thức.
Để hiểu sâu hơn về các tính chất của hình thang cân, các em có thể tham khảo thêm các bài tập tương tự trong sách bài tập và các tài liệu học tập khác. Việc luyện tập thường xuyên sẽ giúp các em nắm vững kiến thức và tự tin giải quyết các bài toán khó hơn.
Ngoài ra, các em cũng có thể tìm hiểu thêm về các loại hình thang khác như hình thang vuông, hình thang thường để có cái nhìn toàn diện hơn về chủ đề này.
Giaitoan.edu.vn hy vọng rằng lời giải chi tiết này sẽ giúp các em học sinh hiểu rõ hơn về bài 10.15 trang 77 sách bài tập Toán 8 - Kết Nối Tri Thức và đạt kết quả tốt trong học tập.