Bài 3.25 trang 42 sách bài tập Toán 8 thuộc chương trình Kết nối tri thức với cuộc sống là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng áp dụng kiến thức về hình học đã học vào giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 3.25 này, giúp các em học sinh nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Cho hình vuông ABCD. Với điểm M nằm giữa C và D, kẻ tia phân giác của góc DAM;
Đề bài
Cho hình vuông ABCD. Với điểm M nằm giữa C và D, kẻ tia phân giác của góc DAM; nó cắt CD ở N. Đường thẳng qua N vuông góc với AM cắt BC ở P. Tính số đo của góc NAP.
Phương pháp giải - Xem chi tiết
Sử dụng tính chất của hình vuông để tính số đo góc NAP: Hình vuông có bốn góc vuông và các cạnh bằng nhau.
Lời giải chi tiết
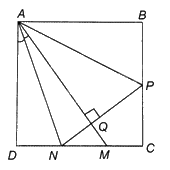
Vì ABCD là hình vuông nên \(\widehat {ADN} = \widehat {ABP} = {90^0}\) và \(AB = AD\)
Gọi Q là giao điểm của NP và AM.
Vì \(NP \bot AM\) tại Q nên \(\widehat {AQN} = \widehat {AQP} = {90^0}\)
Tam giác AND và tam giác ANQ có:
\(\widehat {ADN} = \widehat {AQN} = {90^0}\), AN chung, \(\widehat {DAN} = \widehat {QAN}\) (do AN là tia phân giác của góc DAM)
Do đó, \(\Delta ADN = \Delta AQN\left( {ch - gn} \right)\) nên \(AD = AQ\)
Mà \(AB = AD\) (cmt) nên \(AQ = AB\)
Tam giác AQP và tam giác ABP có:
\(\widehat {AQP} = \widehat {ABP} = {90^0}\), AP chung, \(AQ = AB\) (cmt)
Do đó, \(\Delta AQP = \Delta ABP\left( {ch - cgv} \right)\), suy ra: \(\widehat {QAP} = \widehat {PAB}\)
Ta có: \(\widehat {QAP} + \widehat {PAB} + \widehat {DAN} + \widehat {QAN} = {90^0}\)
Nên \(2\left( {\widehat {QAP} + \widehat {QAN}} \right) = {90^0}\), tức là \(\widehat {NAP} = {45^0}\)
Bài 3.25 trang 42 sách bài tập Toán 8 - Kết nối tri thức với cuộc sống yêu cầu học sinh vận dụng kiến thức về các dấu hiệu nhận biết hai đường thẳng song song để giải quyết bài toán liên quan đến hình học. Để giải bài tập này một cách hiệu quả, trước hết chúng ta cần nắm vững các kiến thức lý thuyết sau:
Đề bài: (Nội dung đề bài sẽ được chèn vào đây - ví dụ: Cho hình vẽ, chứng minh AB song song CD)
Lời giải:
Ví dụ: (Ví dụ cụ thể về cách giải bài tập tương tự)
Trong hình vẽ sau, cho biết góc A = 60° và góc B = 120°. Chứng minh rằng đường thẳng a song song với đường thẳng b.
Lời giải:
Ta có: Góc A + Góc B = 60° + 120° = 180°
Vì góc A và góc B là hai góc trong cùng phía và có tổng bằng 180° nên đường thẳng a song song với đường thẳng b (theo dấu hiệu nhận biết hai đường thẳng song song).
Để củng cố kiến thức về bài 3.25 trang 42, các em học sinh có thể tự giải các bài tập sau:
Khi giải các bài tập về đường thẳng song song, các em cần chú ý:
Giaitoan.edu.vn là website học toán online uy tín, cung cấp lời giải chi tiết, dễ hiểu cho các bài tập Toán từ lớp 6 đến lớp 12. Chúng tôi luôn cập nhật kiến thức mới nhất và phương pháp giải bài tập hiệu quả, giúp các em học sinh học Toán một cách dễ dàng và thú vị.
Hãy truy cập Giaitoan.edu.vn để khám phá thêm nhiều tài liệu học tập hữu ích và cùng chúng tôi chinh phục những thử thách Toán học!