Bài 9.40 trang 60 Sách bài tập Toán 8 - Kết nối tri thức là một bài tập quan trọng trong chương trình học Toán 8. Bài tập này yêu cầu học sinh vận dụng kiến thức về các định lý đã học để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 9.40 trang 60 Sách bài tập Toán 8 - Kết nối tri thức, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Tính chiều cao và diện tích của một tam giác đều có cạnh bằng 4cm.
Đề bài
Tính chiều cao và diện tích của một tam giác đều có cạnh bằng 4cm.
Phương pháp giải - Xem chi tiết
+ Sử dụng kiến thức định lí Pythagore để tính độ dài đường cao: Trong một tam giác vuông, bình phương cạnh huyền bằng tổng các bình phương của hai cạnh góc vuông.
+ Sử dụng tính chất tam giác đều: Trong tam giác đều, đường cao xuất phát từ đỉnh đồng thời là đường trung tuyến.
+ Sử dụng công thức tính diện tích tam giác để tính diện tích tam giác: Diện tích tam giác bằng nửa tích chiều cao nhân với đáy (chiều cao là chiều cao ứng với đáy đó).
Lời giải chi tiết
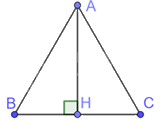
Xét tam giác đều ABC có cạnh \(AB = AC = BC = 4cm\)
Kẻ đường cao AH của tam giác đều ABC.
Khi đó, đường cao AH đồng thời là đường trung tuyến. Do đó, \(AH = \frac{1}{2}BC = \frac{1}{2}.4 = 2\left( {cm} \right)\)
Áp dụng định lý Pythagore vào tam giác ABH vuông tại H có: \(A{H^2} + B{H^2} = A{B^2}\)
\(A{H^2} = A{B^2} - B{H^2} = {4^2} - {2^2} = 12\)
Do đó, \(AH = \sqrt {12} = 2\sqrt 3 \left( {cm} \right)\)
Diện tích tam giác ABC là: \(\frac{1}{2}AH.BC = \frac{1}{2}.4.2\sqrt 3 = 4\sqrt 3 \left( {c{m^2}} \right)\)
Bài 9.40 trang 60 Sách bài tập Toán 8 - Kết nối tri thức thuộc chương trình học Toán 8, tập trung vào việc vận dụng các kiến thức về hình học, đặc biệt là các định lý liên quan đến tứ giác. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững các khái niệm cơ bản và phương pháp giải quyết bài toán hình học.
Trước khi đi vào giải bài, chúng ta cần phân tích kỹ đề bài để xác định rõ yêu cầu và các dữ kiện đã cho. Bài 9.40 thường yêu cầu chứng minh một tính chất nào đó của tứ giác hoặc tính toán các yếu tố liên quan đến tứ giác đó. Việc đọc kỹ đề bài sẽ giúp học sinh tránh được những sai sót không đáng có.
Dưới đây là lời giải chi tiết bài 9.40 trang 60 Sách bài tập Toán 8 - Kết nối tri thức:
(Nội dung lời giải chi tiết bài 9.40 sẽ được trình bày tại đây, bao gồm các bước giải, hình vẽ minh họa và giải thích rõ ràng từng bước. Lời giải cần đảm bảo tính chính xác, logic và dễ hiểu.)
Để giải bài 9.40 trang 60 Sách bài tập Toán 8 - Kết nối tri thức, học sinh cần nắm vững các kiến thức sau:
Để giúp học sinh hiểu rõ hơn về cách giải bài 9.40, chúng ta sẽ xem xét một ví dụ minh họa:
(Ví dụ minh họa sẽ được trình bày tại đây, bao gồm đề bài, lời giải và giải thích chi tiết.)
Để củng cố kiến thức và rèn luyện kỹ năng giải bài tập, học sinh có thể làm thêm các bài tập tương tự sau:
Khi giải bài tập về tứ giác, học sinh cần lưu ý những điều sau:
Bài 9.40 trang 60 Sách bài tập Toán 8 - Kết nối tri thức là một bài tập quan trọng giúp học sinh củng cố kiến thức về tứ giác. Bằng cách nắm vững các khái niệm cơ bản, các định lý liên quan và rèn luyện kỹ năng giải bài tập, học sinh có thể tự tin giải quyết các bài toán hình học một cách hiệu quả.
Giaitoan.edu.vn hy vọng rằng lời giải chi tiết và hướng dẫn giải bài 9.40 trang 60 Sách bài tập Toán 8 - Kết nối tri thức sẽ giúp các em học sinh học tập tốt hơn. Chúc các em thành công!