Bài 3.5 trang 32 sách bài tập Toán 8 Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng giải bài toán thực tế liên quan đến các góc trong tam giác. Bài tập này yêu cầu học sinh vận dụng kiến thức về tổng ba góc trong một tam giác để tìm ra các góc còn lại.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 3.5 trang 32 sách bài tập Toán 8 Kết nối tri thức, giúp các em học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
Cho tứ giác ABCD với AB = BC, CD = DA, (widehat B = {100^ circ }), (widehat D = {120^ circ }). Tính (widehat A) và (widehat C).
Đề bài
Cho tứ giác ABCD với AB = BC, CD = DA, \(\widehat B = {100^ \circ }\), \(\widehat D = {120^ \circ }\). Tính \(\widehat A\) và \(\widehat C\).
Phương pháp giải - Xem chi tiết
Sử dụng tính chất: Trong một tam giác cân, hai góc ở đáy bằng nhau.
Áp dụng định lý tổng 3 góc trong tam giác bằng \({180^ \circ }\).
Áp dụng định lí tổng các góc trong một tứ giác bằng \({360^ \circ }\).
Lời giải chi tiết
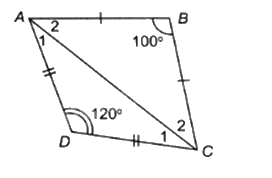
Do AB = BC nên \(\Delta BAC\) cân tại B, suy ra \(\widehat {{A_2}} = \widehat {{C_2}}\).
Do đó \(\widehat {{A_2}} = \widehat {{C_2}} = \frac{{180^\circ - \widehat B}}{2} = \frac{{180^\circ - 100^\circ }}{2} = 40^\circ \).
Do CD = DA, \(\Delta DAC\) cân tại D, suy ra \(\widehat {{A_1}} = \widehat {{C_1}}\)
Xét \(\Delta DAC\) có: \(\widehat {{A_1}} + \widehat {{C_1}} + \widehat D = 180^\circ \)
Do đó \(\widehat {{A_1}} = \widehat {{C_1}} = \frac{{180^\circ - \widehat D}}{2} = \frac{{180^\circ - 120^\circ }}{2} = 30^\circ \).
Ta có: \(\widehat A = \widehat {{A_1}} + \widehat {{A_2}} = 40^\circ + 30^\circ = 70^\circ \)
\(\widehat C = \widehat {{C_1}} + \widehat {{C_2}} = 40^\circ + 30^\circ = 70^\circ \).
Vậy tứ giác ABCD có \(\widehat A = \widehat C = 70^\circ \).
Bài 3.5 trang 32 sách bài tập Toán 8 Kết nối tri thức yêu cầu học sinh giải quyết một bài toán thực tế liên quan đến việc tính toán các góc trong một tam giác. Để giải bài toán này, học sinh cần nắm vững kiến thức về tổng ba góc trong một tam giác bằng 180 độ.
Trước khi bắt đầu giải bài, chúng ta cần đọc kỹ đề bài và xác định rõ những thông tin đã cho và những điều cần tìm. Thông thường, đề bài sẽ cung cấp thông tin về một hoặc hai góc trong tam giác và yêu cầu tính góc còn lại.
Phương pháp giải bài toán này rất đơn giản. Chúng ta chỉ cần áp dụng công thức: Góc thứ ba = 180° - (Góc thứ nhất + Góc thứ hai). Việc xác định đúng góc thứ nhất và góc thứ hai là rất quan trọng để đảm bảo kết quả chính xác.
(Ở đây sẽ là lời giải chi tiết cho bài 3.5 trang 32, bao gồm các bước giải, hình vẽ minh họa nếu cần thiết, và giải thích rõ ràng từng bước. Ví dụ:)
Bài 3.5: Cho tam giác ABC có góc A = 60° và góc B = 80°. Tính góc C.
Giải:
Trong tam giác ABC, ta có:
Góc C = 180° - (Góc A + Góc B)
Góc C = 180° - (60° + 80°)
Góc C = 180° - 140°
Góc C = 40°
Vậy, góc C của tam giác ABC là 40°.
Ngoài bài 3.5, sách bài tập Toán 8 Kết nối tri thức còn có nhiều bài tập tương tự về việc tính toán các góc trong tam giác. Các bài tập này thường có độ khó khác nhau, nhưng phương pháp giải vẫn tương tự. Để làm tốt các bài tập này, học sinh cần luyện tập thường xuyên và nắm vững kiến thức cơ bản.
Kiến thức về tổng ba góc trong một tam giác không chỉ áp dụng trong các bài tập đơn giản mà còn là nền tảng cho nhiều kiến thức nâng cao hơn trong hình học. Ví dụ, kiến thức này được sử dụng để chứng minh các tính chất của tam giác cân, tam giác đều, và các loại tam giác đặc biệt khác.
Bài 3.5 trang 32 sách bài tập Toán 8 Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng giải bài toán thực tế về các góc trong tam giác. Bằng cách nắm vững kiến thức cơ bản và luyện tập thường xuyên, học sinh có thể tự tin giải quyết các bài tập tương tự và đạt kết quả tốt trong môn Toán.
| Góc A | Góc B | Góc C |
|---|---|---|
| 60° | 80° | 40° |
| 70° | 50° | 60° |
| Tổng ba góc luôn bằng 180° | ||