Bài 3.3 trang 32 sách bài tập Toán 8 - Kết nối tri thức với cuộc sống là một bài tập quan trọng trong chương trình học Toán 8. Bài tập này yêu cầu học sinh vận dụng kiến thức đã học về các phép biến đổi đại số để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 3.3 trang 32 sách bài tập Toán 8 - Kết nối tri thức với cuộc sống, giúp các em học sinh nắm vững kiến thức và tự tin làm bài tập.
Chứng minh tổng độ dài hai đường chéo của tứ giác:
Đề bài
Chứng minh tổng độ dài hai đường chéo của tứ giác:
a) Bé hơn chu vi của tứ giác;
b) Lớn hơn tổng hai cạnh đối tùy ý của tứ giác, từ đó lớn hơn nửa chu vi của tứ giác.
Phương pháp giải - Xem chi tiết
Áp dụng định lý bất đẳng thức trong tam giác.
Lời giải chi tiết
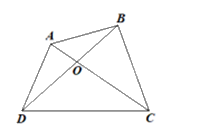
Xét tứ giác ABCD. Chu vi tứ giác ABCD là \({P_{ABCD}}\; = AB + BC + CD + DA\).
a) Trong \(\Delta ABC\) có \(AC < AB + BC\) (bất đẳng thức trong tam giác)
Trong \(\Delta ACD\) có \(AC < CD + DA\) (bất đẳng thức trong tam giác)
Do đó \(AC + AC < AB + BC + \;CD + DA\) hay \(2AC < {P_{ABCD}}\;\) (1)
Tương tự, trong \(\Delta ABD\) có \(BD < AD + AB\)
Trong \(\Delta BCD\) có: \(BD < CD + BC\)
Do đó \(BD + BD < AD + AB + CD + BC\) hay \(2BD < {P_{ABCD}}\). (2)
Từ (1) và (2) suy ra \(2\left( {AC + BD} \right) < 2{P_{ABCD}}\), do đó \(AC + BD < {P_{ABCD}}\).
b) Gọi O là giao điểm của AC và BD.
Trong \(\Delta OAB\) có \(OA + OB > AB\) (bất đẳng thức trong tam giác)
Trong \(\Delta OCD\) có \(OC + OD > CD\) (bất đẳng thức trong tam giác)
Nên \(AC + BD = OA + OC + OB + OD > AB + CD\).
Trong \(\Delta OAD\) có \(OA + OD > AD\) (bất đẳng thức trong tam giác)
Trong \(\Delta OBC\) có \(OB + OC > BC\) (bất đẳng thức trong tam giác)
Nên \(AC + BD = OA + OC + OB + OD > AD + BC\).
Vậy \(2\left( {AC + BD} \right) > AB + BC + CD + DA = {P_{ABCD}}\)
Tức là \(AC + BD\; > \frac{1}{2}{P_{ABCD}}\) (đpcm).
Bài 3.3 trang 32 sách bài tập Toán 8 - Kết nối tri thức với cuộc sống thuộc chương trình học Toán 8, tập trung vào việc vận dụng các kiến thức về đa thức, phân thức và các phép toán trên chúng. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững các khái niệm cơ bản và các quy tắc biến đổi đại số.
Trước khi đi vào giải bài, chúng ta cùng xem lại đề bài và yêu cầu của bài 3.3 trang 32 sách bài tập Toán 8 - Kết nối tri thức với cuộc sống:
(Giả sử đề bài là: Phân tích các đa thức sau thành nhân tử: a) x2 - 4; b) x2 + 4x + 4; c) x3 - 8)
Để giải bài tập này, chúng ta sẽ sử dụng các phương pháp phân tích đa thức thành nhân tử sau:
Lời giải:
Khi giải các bài tập phân tích đa thức thành nhân tử, học sinh cần lưu ý những điều sau:
Để củng cố kiến thức và rèn luyện kỹ năng, các em có thể tự giải các bài tập tương tự sau:
Bài 3.3 trang 32 sách bài tập Toán 8 - Kết nối tri thức với cuộc sống là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng phân tích đa thức thành nhân tử. Hy vọng với lời giải chi tiết và những lưu ý trên, các em học sinh sẽ tự tin hơn khi giải bài tập này và đạt kết quả tốt trong môn Toán 8.
Giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán. Chúc các em học tập tốt!