Bài 7.21 trang 27 sách bài tập Toán 8 - Kết nối tri thức với cuộc sống là một bài tập quan trọng trong chương trình học Toán 8. Bài tập này yêu cầu học sinh vận dụng kiến thức đã học về các góc trong tam giác để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 7.21 trang 27, giúp các em học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
Hàm số \(y = f\left( x \right)\) được cho trong bảng sau:
Đề bài
Hàm số \(y = f\left( x \right)\) được cho trong bảng sau:

Vẽ đồ thị của hàm số \(y = f\left( x \right)\)
Phương pháp giải - Xem chi tiết
Sử dụng khái niệm đồ thị của hàm số để vẽ đồ thị hàm số: Đồ thị của hàm số \(y = f\left( x \right)\) là tập hợp tất cả các điểm biểu diễn các cặp giá trị tương ứng (x; y) trên mặt phẳng tọa độ.
Lời giải chi tiết
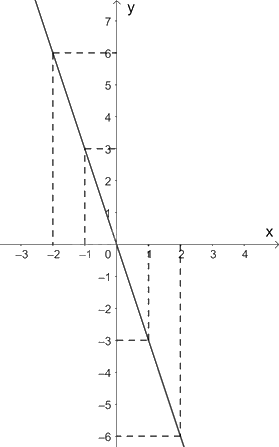
Đồ thị hàm số \(y = f\left( x \right)\) đi qua các điểm (-2; 6); (-1; 3); (0;0); (1; -3); (2; -6)
Bài 7.21 trang 27 sách bài tập Toán 8 - Kết nối tri thức với cuộc sống là một bài toán thực tế, yêu cầu học sinh áp dụng kiến thức về tổng ba góc trong một tam giác. Để giải bài toán này, chúng ta cần hiểu rõ các khái niệm và định lý liên quan.
Bài toán thường yêu cầu tính một góc của tam giác khi biết hai góc còn lại, hoặc tính góc ngoài của tam giác khi biết các góc trong. Đôi khi, bài toán có thể yêu cầu chứng minh một tính chất liên quan đến các góc trong tam giác.
(Giả sử bài toán cụ thể là: Cho tam giác ABC có góc A = 60 độ, góc B = 80 độ. Tính góc C.)
Giải:
Áp dụng định lý về tổng ba góc trong một tam giác, ta có:
Góc A + Góc B + Góc C = 180 độ
60 độ + 80 độ + Góc C = 180 độ
140 độ + Góc C = 180 độ
Góc C = 180 độ - 140 độ
Góc C = 40 độ
Vậy, góc C của tam giác ABC bằng 40 độ.
Ngoài bài toán tính góc trong tam giác, còn có các dạng bài tập liên quan đến góc ngoài của tam giác. Để giải các bài tập này, chúng ta cần sử dụng mối quan hệ giữa góc ngoài và góc trong của tam giác.
Ví dụ:
Kiến thức về góc trong tam giác có ứng dụng rộng rãi trong thực tế, đặc biệt trong các lĩnh vực như kiến trúc, xây dựng, hàng hải và thiên văn học. Ví dụ, trong kiến trúc, các kiến trúc sư sử dụng kiến thức về góc trong tam giác để thiết kế các công trình đảm bảo tính thẩm mỹ và độ bền vững.
Để củng cố kiến thức về góc trong tam giác, các em học sinh có thể tự giải thêm các bài tập sau:
Bài 7.21 trang 27 sách bài tập Toán 8 - Kết nối tri thức với cuộc sống là một bài tập quan trọng, giúp học sinh hiểu rõ hơn về các góc trong tam giác và ứng dụng của chúng trong thực tế. Hy vọng với lời giải chi tiết và hướng dẫn giải bài tập trên, các em học sinh sẽ tự tin hơn khi làm bài tập Toán 8.