Bài 9.47 trang 63 Sách bài tập Toán 8 - Kết nối tri thức là một bài tập quan trọng trong chương trình học Toán 8. Bài tập này yêu cầu học sinh vận dụng kiến thức về các định lý đã học để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 9.47 trang 63 Sách bài tập Toán 8 - Kết nối tri thức, giúp các em học sinh hiểu rõ bản chất của bài toán và tự tin làm bài tập.
Cho tam giác nhọn ABC có các đường cao AD, BE, CF cắt nhau ở H. Chứng minh rằng: a) (HA.HD = HB.HE = HC.HF);
Đề bài
Cho tam giác nhọn ABC có các đường cao AD, BE, CF cắt nhau ở H. Chứng minh rằng:
a) \(HA.HD = HB.HE = HC.HF\);
b) $\Delta AFC\backsim \Delta AEB$ và $AF.AB=AE.AC\,;$
c) $\Delta BDF\backsim \Delta EDC$ và DA là tia phân giác của góc EDF.
Phương pháp giải - Xem chi tiết
+ Sử dụng kiến thức trường hợp đồng dạng của tam giác vuông để chứng minh: Nếu một góc nhọn của tam giác vuông này bằng một góc nhọn của tam giác vuông kia thì hai tam giác vuông đó đồng dạng với nhau.
+ Sử dụng kiến thức về trường hợp đồng dạng của tam giác để chứng minh: Nếu hai cạnh của tam giác này tỉ lệ với hai cạnh của tam giác kia và góc tạo bởi các cặp cạnh đó bằng nhau thì hai tam giác đó đồng dạng với nhau.
Lời giải chi tiết
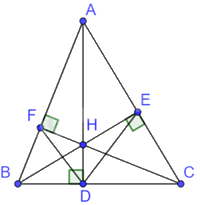
a) Vì AD, BE, CF là các đường cao của tam giác ABC nên \(AD \bot BC,BE \bot AC,CF \bot AB\)
nên \(\widehat {AEB} = \widehat {BEC} = \widehat {ADB} = \widehat {ADC} = \widehat {CFA} = \widehat {CFB} = {90^0}\)
Tam giác AHE và tam giác BHD có:
\(\widehat {AEH} = \widehat {HDB} = {90^0}\) (cmt), \(\widehat {AHE} = \widehat {BHD}\) (hai góc đối đỉnh). Do đó, $\Delta AHE\backsim \Delta BHD\left( g-g \right)$
Suy ra: \(\frac{{AH}}{{BH}} = \frac{{HE}}{{HD}}\) nên \(HA.HD = HB.HE\) (1)
Tam giác HBF và tam giác HCE có:
\(\widehat {HFB} = \widehat {HEC} = {90^0}\) (cmt), \(\widehat {BHF} = \widehat {EHC}\) (hai góc đối đỉnh). Do đó, $\Delta HBF\backsim \Delta HCE\left( g-g \right)$
Suy ra: \(\frac{{HB}}{{HC}} = \frac{{HF}}{{HE}}\) nên \(HB.HE = HC.HF\) (2)
Từ (1) và (2) ta có: \(HA.HD = HB.HE = HC.HF\)
b) Tam giác AFC và tam giác AEB có:
\(\widehat {AFC} = \widehat {AEC} = {90^0},\widehat {BAC}\;chung\)
Do đó, $\Delta AFC\backsim \Delta AEB\left( g-g \right)$
Suy ra: \(\frac{{AF}}{{AE}} = \frac{{AC}}{{AB}}\) nên \(AF.AB = AE.AC\,\)
c) Vì \(HA.HD = HB.HE\) nên \(\frac{{HA}}{{HE}} = \frac{{HB}}{{HD}}\)
Tam giác HAB và tam giác HED có: \(\frac{{HA}}{{HE}} = \frac{{HB}}{{HD}}\) (cmt), \(\widehat {AHB} = \widehat {HED}\) (hai góc đối đỉnh)
Do đó, $\Delta AHB\backsim \Delta EHD\left( c-g-c \right)$, suy ra: \(\widehat {HAB} = \widehat {HED}\)
Mà \(\widehat {HAB} + \widehat {FBD} = \widehat {HED} + \widehat {DEC}\left( { = {{90}^0}} \right)\)
Do đó, \(\widehat {FBD} = \widehat {DEC}\)
Chứng minh tương tự ta có: \(\widehat {BFD} = \widehat {ECD}\)
Tam giác BDF và tam giác EDC có: \(\widehat {FBD} = \widehat {DEC}\) (cmt), \(\widehat {BFD} = \widehat {ECD}\) (cmt). Do đó, $\Delta BDF\backsim \Delta EDC\left( g-g \right)$
Suy ra: \(\widehat {BDF} = \widehat {EDC}\)
Mà \(\widehat {BDF} + \widehat {FDH} = \widehat {EDC} + \widehat {HDE}\left( { = {{90}^0}} \right)\)
Do đó, \(\widehat {FDH} = \widehat {HDE}\)
Vậy DA là tia phân giác của góc EDF
Bài 9.47 trang 63 Sách bài tập Toán 8 - Kết nối tri thức thuộc chương trình học Toán 8, tập trung vào việc vận dụng các kiến thức về hình học, đặc biệt là các định lý liên quan đến tứ giác và các tính chất của đường trung bình trong tam giác. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững lý thuyết và biết cách áp dụng vào thực tế.
Trước khi bắt đầu giải bài tập, điều quan trọng là phải đọc kỹ đề bài và xác định rõ yêu cầu của bài toán. Bài 9.47 thường yêu cầu chứng minh một đẳng thức, tính toán độ dài đoạn thẳng, hoặc xác định tính chất của một hình nào đó. Việc phân tích đề bài sẽ giúp học sinh có định hướng rõ ràng trong quá trình giải.
Để cung cấp lời giải chi tiết, chúng ta cần xem xét cụ thể nội dung của bài tập. Giả sử bài tập yêu cầu chứng minh một tứ giác là hình bình hành, ta cần chứng minh hai cặp cạnh đối song song hoặc một cặp cạnh đối song song và bằng nhau. Hoặc, nếu bài tập yêu cầu tính độ dài đoạn thẳng, ta cần sử dụng các định lý về tam giác đồng dạng hoặc các công thức tính toán liên quan.
Ví dụ, nếu bài toán cho một tứ giác ABCD với các điểm M, N, P, Q lần lượt là trung điểm của các cạnh AB, BC, CD, DA. Yêu cầu chứng minh MNPQ là hình bình hành. Ta có thể chứng minh bằng cách sử dụng tính chất đường trung bình của tam giác. Cụ thể:
Từ đó suy ra MN // PQ và MN = PQ, do đó MNPQ là hình bình hành.
Ngoài bài 9.47, còn rất nhiều bài tập tương tự trong sách bài tập Toán 8 - Kết nối tri thức. Các bài tập này thường yêu cầu học sinh vận dụng các kiến thức về:
Để giải các bài tập này, học sinh cần:
Để học Toán 8 hiệu quả, học sinh nên:
Bài 9.47 trang 63 Sách bài tập Toán 8 - Kết nối tri thức là một bài tập quan trọng giúp học sinh củng cố kiến thức về hình học. Bằng cách nắm vững lý thuyết, phân tích đề bài và áp dụng các kiến thức đã học, học sinh có thể giải bài tập một cách hiệu quả và tự tin. Giaitoan.edu.vn hy vọng rằng lời giải chi tiết và hướng dẫn giải bài tập này sẽ giúp các em học sinh học Toán 8 tốt hơn.