Bài 3.6 trang 32 sách bài tập Toán 8 - Kết nối tri thức với cuộc sống là một bài tập quan trọng trong chương trình học Toán 8. Bài tập này yêu cầu học sinh vận dụng kiến thức đã học về các phép biến đổi đại số để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 3.6 trang 32 sách bài tập Toán 8 - Kết nối tri thức với cuộc sống, giúp các em học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
a) Góc kề bù với góc tại một đỉnh của tứ giác gọi là một góc ngoài tại đỉnh đo của tứ giác.
Đề bài
a) Góc kề bù với góc tại một đỉnh của tứ giác gọi là một góc ngoài tại đỉnh đo của tứ giác. (Có hai góc ngoài tại một đỉnh của tứ giác, chúng đối đỉnh nên thường được gọi tắt là góc ngoài tại đỉnh đó của tứ giác). Hãy tính tổng bốn góc ngoài tại bốn đỉnh của một tứ giác.
b) Định nghĩa góc ngoài tại một đỉnh của một tam giác tương tư. Hỏi tổng các góc ngoài của một tam giác bằng bao nhiêu?
Phương pháp giải - Xem chi tiết
Áp dụng định lý tổng 3 góc trong tam giác bằng \({180^ \circ }\).
Áp dụng định lí tổng các góc trong một tứ giác bằng \({360^ \circ }\).
Áp dụng tính chất hai góc kề bù có tổng bằng \({180^ \circ }\).
Lời giải chi tiết
a)
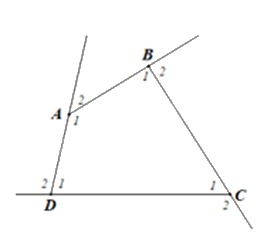
Do góc ngoài và góc tại đỉnh đó là 2 góc kề bù nên tổng bằng \(180^\circ \).
Xét tứ giác ABCD (hình vẽ) có: \(\widehat {{A_1}} + \widehat {{B_1}} + \widehat {{C_1}} + \widehat {{D_1}} = 360^\circ \)
Góc ngoài tại đỉnh A là \(\widehat {{A_2}} = 180^\circ - \widehat {{A_1}}\);
Góc ngoài tại đỉnh B là \(\widehat {{B_2}} = 180^\circ - \widehat {{B_1}}\);
Góc ngoài tại đỉnh C là \(\widehat {{C_2}} = 180^\circ - \widehat {{C_1}}\);
Góc ngoài tại đỉnh D là \(\widehat {{D_2}} = 180^\circ - \widehat {{D_1}}\).
Tổng 4 góc ngoài của tứ giác ABCD là:
\(\widehat {{A_2}} + \widehat {{B_2}} + \widehat {{C_2}} + \widehat {{D_2}}\)
\( = \left( {180^\circ - \widehat {{A_1}}} \right) + \left( {180^\circ - \widehat {{B_1}}} \right) + \left( {180^\circ - \widehat {{C_1}}} \right) + \left( {180^\circ - \widehat {{D_1}}} \right)\)
\( = 4.180^\circ - \left( {\widehat {{A_1}} + \widehat {{B_1}} + \widehat {{C_1}} + \widehat {{D_1}}} \right)\)
\( = 720^\circ - 360^\circ = 360^\circ \).
b)
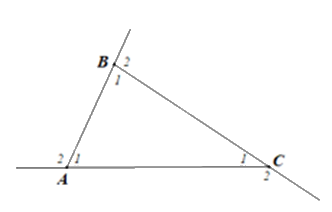
Tương tự, với tam giác ABC, ta có tổng các góc ngoài là:
\(\widehat {{A_2}} + \widehat {{B_2}} + \widehat {{C_2}}\)\( = \left( {180^\circ - \widehat {{A_1}}} \right) + \left( {180^\circ - \widehat {{B_1}}} \right) + \left( {180^\circ - \widehat {{C_1}}} \right)\)
\( = 3.180^\circ - \left( {\widehat {{A_1}} + \widehat {{B_1}} + \widehat {{C_1}}} \right)\)\( = 540^\circ - 180^\circ = 360^\circ \).
Bài 3.6 trang 32 sách bài tập Toán 8 - Kết nối tri thức với cuộc sống thuộc chương trình học Toán 8, tập trung vào việc vận dụng các kiến thức về đa thức, phân thức và các phép toán trên chúng để giải quyết các bài toán thực tế. Bài tập này không chỉ giúp học sinh củng cố kiến thức mà còn rèn luyện kỹ năng tư duy logic và khả năng giải quyết vấn đề.
Bài tập 3.6 thường bao gồm các dạng bài sau:
Để giải bài 3.6 trang 32 sách bài tập Toán 8 - Kết nối tri thức với cuộc sống một cách hiệu quả, các em cần nắm vững các kiến thức sau:
Ví dụ minh họa:
Giả sử bài tập 3.6 yêu cầu chúng ta rút gọn biểu thức sau:
(x2 - 4) / (x + 2)
Lời giải:
Chúng ta có thể phân tích tử số thành nhân tử:
x2 - 4 = (x - 2)(x + 2)
Vậy biểu thức trở thành:
((x - 2)(x + 2)) / (x + 2)
Với điều kiện x ≠ -2, chúng ta có thể rút gọn biểu thức thành:
x - 2
Để học tốt Toán 8, các em có thể tham khảo các tài liệu sau:
Bài 3.6 trang 32 sách bài tập Toán 8 - Kết nối tri thức với cuộc sống là một bài tập quan trọng giúp các em củng cố kiến thức và rèn luyện kỹ năng giải toán. Hy vọng với hướng dẫn chi tiết và các mẹo giải bài tập hiệu quả mà giaitoan.edu.vn cung cấp, các em sẽ tự tin chinh phục bài tập này và đạt kết quả tốt trong môn Toán.