Chào mừng các em học sinh đến với bài giải bài 9.46 trang 63 sách bài tập Toán 8 - Kết nối tri thức. Bài viết này sẽ cung cấp cho các em lời giải chi tiết, dễ hiểu, giúp các em nắm vững kiến thức và kỹ năng giải toán.
Giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán. Hãy cùng chúng tôi khám phá lời giải của bài tập này nhé!
Cho tam giác ABC vuông tại A có đường cao AH. Biết rằng \(AB = 6cm\) và \(AC = 8cm\), hãy tính độ dài các đoạn thẳng BC, AH, BH, CH.
Đề bài
Cho tam giác ABC vuông tại A có đường cao AH. Biết rằng \(AB = 6cm\) và \(AC = 8cm\), hãy tính độ dài các đoạn thẳng BC, AH, BH, CH.
Phương pháp giải - Xem chi tiết
+ Sử dụng kiến thức trường hợp đồng dạng của tam giác vuông để tính CH, AH: Nếu một góc nhọn của tam giác vuông này bằng một góc nhọn của tam giác vuông kia thì hai tam giác vuông đó đồng dạng với nhau.
+ Sử dụng kiến thức định lí Pythagore để tính độ dài BC: Trong một tam giác vuông, bình phương cạnh huyền bằng tổng các bình phương của hai cạnh góc vuông.
Lời giải chi tiết
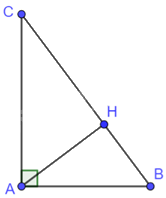
Tam giác ABC vuông tại A nên \(\widehat {BAC} = {90^0}\)
Áp dụng định lý Pythagore vào tam giác ABC vuông tại A ta có: \(B{C^2} = A{B^2} + A{C^2} = {6^2} + {8^2} = 100\) nên \(BC = 10cm\)
Vì AH là đường cao trong tam giác ABC nên \(AH \bot BC\).
Do đó, \(\widehat {AHB} = \widehat {AHC} = {90^0}\)
Tam giác ABC và tam giác HAC có: \(\widehat {BAC} = \widehat {AHC} = {90^0},\widehat C\) chung. Do đó, $\Delta ABC\backsim \Delta HAC\left( g-g \right)$
Suy ra: \(\frac{{AC}}{{HC}} = \frac{{BC}}{{AC}}\) nên \(CH = \frac{{C{A^2}}}{{CB}} = \frac{{{8^2}}}{{10}} = \frac{{32}}{5}\left( {cm} \right)\)
Do đó, \(BH = BC - CH = 10 - \frac{{32}}{5} = \frac{{18}}{5}\left( {cm} \right)\)
Vì $\Delta ABC\backsim \Delta HAC\left( cmt \right)$ nên \(\frac{{AB}}{{HA}} = \frac{{BC}}{{AC}}\)
Do đó, \(AH = \frac{{AB.AC}}{{BC}} = \frac{{6.8}}{{10}} = \frac{{24}}{5}\left( {cm} \right)\)
Bài 9.46 trang 63 sách bài tập Toán 8 - Kết nối tri thức thuộc chương trình học Toán 8, tập trung vào việc vận dụng các kiến thức về hình học, cụ thể là các tính chất của hình thang cân và ứng dụng vào giải quyết các bài toán thực tế.
Trước khi đi vào giải bài tập, chúng ta cần ôn lại một số kiến thức lý thuyết quan trọng:
Bài toán 9.46 yêu cầu chúng ta vận dụng các kiến thức về hình thang cân để tính toán các yếu tố hình học như độ dài cạnh, góc, đường cao. Để giải bài toán này một cách hiệu quả, chúng ta cần:
(Ở đây sẽ là lời giải chi tiết của bài toán 9.46, bao gồm các bước giải, hình vẽ minh họa và giải thích rõ ràng. Ví dụ:)
Đề bài: Cho hình thang cân ABCD (AB // CD), AB = 6cm, CD = 10cm, AD = BC = 5cm. Tính chiều cao của hình thang.
Lời giải:
Kẻ AH và BK vuông góc với CD (H, K thuộc CD). Khi đó, AH = BK là chiều cao của hình thang.
Vì ABCD là hình thang cân nên DH = KC = (CD - AB) / 2 = (10 - 6) / 2 = 2cm.
Xét tam giác vuông ADH, ta có: AH2 = AD2 - DH2 = 52 - 22 = 21.
Vậy, AH = √21 cm. Do đó, chiều cao của hình thang ABCD là √21 cm.
Ngoài bài 9.46, còn rất nhiều bài tập tương tự về hình thang cân. Để giải quyết các bài tập này, các em có thể tham khảo các phương pháp sau:
Để củng cố kiến thức, các em có thể tự giải các bài tập sau:
Bài 9.46 trang 63 sách bài tập Toán 8 - Kết nối tri thức là một bài tập quan trọng giúp các em hiểu sâu hơn về hình thang cân và ứng dụng vào giải quyết các bài toán thực tế. Hy vọng với lời giải chi tiết và các phương pháp giải được trình bày trong bài viết này, các em sẽ tự tin hơn trong việc học tập môn Toán.