Bài 8.13 trang 45 sách bài tập Toán 8 thuộc chương trình Kết nối tri thức với cuộc sống là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng áp dụng kiến thức về hình hộp chữ nhật và hình lập phương vào giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 8.13, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Một cửa hàng điện máy thống kê lại số lượng các mặt hàng bán trong năm qua như bảng sau:
Đề bài
Một cửa hàng điện máy thống kê lại số lượng các mặt hàng bán trong năm qua như bảng sau:
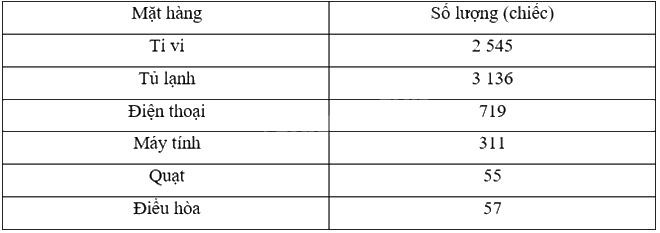
a) Tính xác suất thực nghiệm tiêu thụ mỗi mặt hàng của cửa hàng.
b) Giả sử năm sau cửa hàng bán được tổng số 7 500 chiếc các loại. Hãy dự đoán trong đó có:
Phương pháp giải - Xem chi tiết
+ Sử dụng kiến thức xác suất thực nghiệm của một biến cố để tính: Giả sử trong n lần thực nghiệm hoặc n lần theo dõi (quan sát) một hiện tượng ta thấy biến cố E xảy ra k lần. Khi đó xác suất thực nghiệm của biến cố E bằng \(\frac{k}{n}\), tức là bằng tỉ số giữa số lần xuất hiện biến cố E và số lần thực hiện thực nghiệm hoặc theo dõi hiện tượng đó.
+ Sử dụng mối liên hệ giữa xác suất thực nghiệm với xác suất: Xác suất của biến cố E được ước lượng bằng xác suất thực nghiệm của E: \(P\left( E \right) \approx \frac{k}{n};\)trong đó n là số lần thực nghiệm hay theo dõi một hiện tượng, k là số lần biến cố E xảy ra.
Lời giải chi tiết
a) Trong năm vừa qua, cửa hàng bán được tổng số mặt hàng là: \(2\;545 + 3\;136 + 719 + 311 + 55 + 57 = 6\;823\)
Xác suất thực nghiệm khi tiêu thụ ti vi là: \(\frac{{2\;545}}{{6\;823}}\)
Xác suất thực nghiệm khi tiêu thụ tủ lạnh là: \(\frac{{3\;136}}{{6\;823}}\)
Xác suất thực nghiệm khi tiêu thụ điện thoại là: \(\frac{{719}}{{6\;823}}\)
Xác suất thực nghiệm khi tiêu thụ máy tính là: \(\frac{{311}}{{6\;823}}\)
Xác suất thực nghiệm khi tiêu thụ quạt là: \(\frac{{55}}{{6\;823}}\)
Xác suất thực nghiệm khi tiêu thụ điều hòa là: \(\frac{{57}}{{6\;823}}\)
b) Gọi k là số chiếc ti vi cửa hàng bán được trong năm sau.
Ta có: \(\frac{k}{{7\;500}} \approx \frac{{2545}}{{6823}}\) nên \(k \approx \frac{{7\;500.2\;545}}{{6\;823}} \approx 2797,52\)
Do đó, ta dự đoán có khoảng 2 798 chiếc ti vi cửa hàng bán được trong năm sau.
Gọi h là số chiếc tủ lạnh, quạt hoặc điều hòa cửa hàng bán được trong năm sau.
Ta có: \(\frac{h}{{7\;500}} \approx \frac{{3\;136 + 55 + 57}}{{6\;823}} = \frac{{3\;248}}{{6\;823}}\) nên \(h \approx \frac{{7\;500.3\;248}}{{6\;823}} \approx 3\;570,28\)
Do đó, ta dự đoán có khoảng 3 570 chiếc tủ lạnh, quạt hoặc điều hòa cửa hàng bán được trong năm sau.
Bài 8.13 yêu cầu chúng ta giải quyết một bài toán liên quan đến hình hộp chữ nhật và hình lập phương, cụ thể là tính toán thể tích và diện tích bề mặt. Để giải bài toán này một cách hiệu quả, chúng ta cần nắm vững các công thức cơ bản:
Trước khi bắt tay vào giải bài toán, chúng ta cần đọc kỹ đề bài để hiểu rõ yêu cầu và các dữ kiện đã cho. Thông thường, đề bài sẽ cung cấp các thông tin về kích thước của hình hộp chữ nhật hoặc hình lập phương, và yêu cầu chúng ta tính toán thể tích, diện tích bề mặt, hoặc các thông số liên quan khác.
(Giả sử đề bài là: Một hình hộp chữ nhật có chiều dài 5cm, chiều rộng 4cm và chiều cao 3cm. Tính thể tích và diện tích bề mặt của hình hộp chữ nhật đó.)
Giải:
Thể tích của hình hộp chữ nhật là:
V = 5cm * 4cm * 3cm = 60cm3
Diện tích bề mặt của hình hộp chữ nhật là:
S = 2 * (5cm * 4cm + 4cm * 3cm + 3cm * 5cm) = 2 * (20cm2 + 12cm2 + 15cm2) = 2 * 47cm2 = 94cm2
Vậy, thể tích của hình hộp chữ nhật là 60cm3 và diện tích bề mặt là 94cm2.
Ngoài bài 8.13, còn rất nhiều bài tập tương tự liên quan đến hình hộp chữ nhật và hình lập phương. Các bài tập này có thể yêu cầu chúng ta:
Để giải các bài tập này, chúng ta cần:
Để củng cố kiến thức và kỹ năng giải bài tập về hình hộp chữ nhật và hình lập phương, các em học sinh nên luyện tập thêm với các bài tập khác trong sách bài tập và các tài liệu tham khảo khác. Ngoài ra, các em cũng có thể tìm kiếm các bài giảng trực tuyến hoặc tham gia các khóa học toán online để được hướng dẫn và giải đáp thắc mắc.
Bài 8.13 trang 45 sách bài tập Toán 8 - Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng giải toán về hình hộp chữ nhật và hình lập phương. Bằng cách nắm vững các công thức cơ bản, phân tích đề bài một cách cẩn thận và luyện tập thường xuyên, các em học sinh có thể tự tin giải quyết các bài tập tương tự và đạt kết quả tốt trong môn Toán.