Bài 3.4 trang 32 sách bài tập Toán 8 - Kết nối tri thức với cuộc sống là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng áp dụng các kiến thức đã học về hình học. Bài tập này thường yêu cầu học sinh phân tích hình, chứng minh các tính chất liên quan đến hình bình hành, hình chữ nhật, hình thoi, hình vuông.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 3.4 trang 32 sách bài tập Toán 8 - Kết nối tri thức với cuộc sống, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Tìm điểm M bên trong tứ giác ABCD sao cho tổng khoảng cách từ M đến bốn đỉnh A, B, C, D là bé nhất.
Đề bài
Tìm điểm M bên trong tứ giác ABCD sao cho tổng khoảng cách từ M đến bốn đỉnh A, B, C, D là bé nhất.
Phương pháp giải - Xem chi tiết
Sử dụng bất đẳng thức tam giác: Trong một tam giác, tổng hai cạnh luôn lớn hơn cạnh còn lại
Lời giải chi tiết
Trước hết cho hai điểm phân biệt P, Q thì với mọi điểm M ta có \(MP + MQ \ge PQ\) và \(MP + MQ = PQ\) chỉ khi M thuộc đoạn thẳng PQ.
Thật vậy,
• Nếu M không thuộc đường thẳng PQ thì \(MP + MQ > PQ\) (bất đẳng thức tam giác) (hình vẽ)
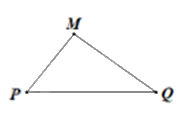
• Nếu M thuộc đoạn thẳng PQ thì \(MP + MQ = PQ\) (hình vẽ)
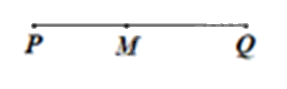
• Nếu M thuộc đường thẳng PQ nhưng không thuộc đoạn thẳng PQ thì hoặc P nằm giữa M và Q hoặc Q nằm giữa P và M, dễ thấy trong cả hai trường hợp đó, \(MP + MQ > PQ\) (hình vẽ).
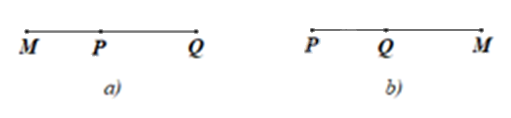
– Xét điểm M tuỳ ý trong tứ giác ABCD (hình vẽ).
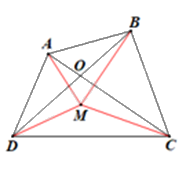
Ta có:
\(MA + MC \ge AC\) và \(MA + MC = AC\) khi điểm M nằm trên đoạn thẳng AC.
\(MB + MD \ge BD\) và \(MB + MD = BD\) khi điểm M nằm trên đoạn thẳng BD.
Do đó \(MA + MB + MC + MD \ge AC + BD\) và \(MA + MB + MC + MD = AC + BD\) chỉ khi M vừa thuộc đoạn thẳng AC vừa thuộc đoạn thẳng BD tức là M phải trùng với giao điểm O của AC và BD.
Bài 3.4 trang 32 sách bài tập Toán 8 - Kết nối tri thức với cuộc sống thuộc chương 3: Các hình bình hành – Hình chữ nhật – Hình thoi – Hình vuông. Bài tập này thường xoay quanh việc chứng minh các tính chất của các hình đặc biệt này, đặc biệt là liên quan đến các đường chéo, góc và cạnh.
Bài tập 3.4 thường yêu cầu học sinh:
Để giải bài 3.4 trang 32 sách bài tập Toán 8 - Kết nối tri thức với cuộc sống, chúng ta cần nắm vững các kiến thức sau:
(Giả sử đề bài cụ thể của bài 3.4 là: Cho hình chữ nhật ABCD, gọi O là giao điểm của hai đường chéo. Chứng minh rằng OA = OB = OC = OD.)
Vì ABCD là hình chữ nhật nên AC = BD (tính chất đường chéo của hình chữ nhật).
O là giao điểm của hai đường chéo AC và BD nên OA = OC = AC/2 và OB = OD = BD/2 (tính chất giao điểm của đường chéo).
Do đó, OA = OC = AC/2 = BD/2 = OB = OD.
Vậy OA = OB = OC = OD (điều phải chứng minh).
Để hiểu sâu hơn về các tính chất của hình chữ nhật, hình thoi, hình vuông, các em có thể làm thêm các bài tập sau:
Khi giải các bài tập hình học, các em nên:
Giaitoan.edu.vn hy vọng với lời giải chi tiết và những hướng dẫn trên, các em học sinh sẽ tự tin hơn khi giải bài tập 3.4 trang 32 sách bài tập Toán 8 - Kết nối tri thức với cuộc sống và các bài tập tương tự. Chúc các em học tốt!
| Hình | Tính chất |
|---|---|
| Hình bình hành | Các cạnh đối song song và bằng nhau, các góc đối bằng nhau, hai đường chéo cắt nhau tại trung điểm của mỗi đường. |
| Hình chữ nhật | Có bốn góc vuông, hai đường chéo bằng nhau và cắt nhau tại trung điểm của mỗi đường. |
| Hình thoi | Có bốn cạnh bằng nhau, hai đường chéo vuông góc với nhau và cắt nhau tại trung điểm của mỗi đường. |
| Hình vuông | Có bốn cạnh bằng nhau và bốn góc vuông, hai đường chéo bằng nhau, vuông góc với nhau và cắt nhau tại trung điểm của mỗi đường. |