Bài 6.26 trang 10 sách bài tập Toán 8 Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng giải toán thực tế. Bài tập này thường liên quan đến việc ứng dụng các kiến thức về hình học, đại số đã học vào các tình huống cụ thể.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 6.26 trang 10, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Cho hai hình hộp chữ nhật bằng nhau có cùng thể tích (200c{m^3}) và một hình hộp chữ nhật có thể tích (500c{m^3})
Đề bài
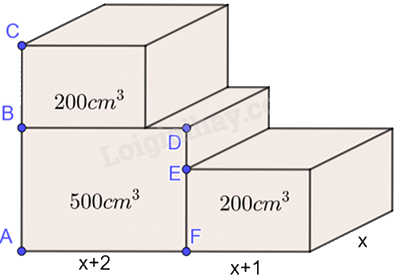
Cho hai hình hộp chữ nhật bằng nhau có cùng thể tích \(200c{m^3}\) và một hình hộp chữ nhật có thể tích \(500c{m^3}\) sắp xếp như trong hình bên (độ dài các cạnh hình hộp được tính bằng đơn vị cm). Viết các phân thức biểu thị độ dài (tính bằng cm) của các đoạn thẳng AC và DE.
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức cộng (trừ) các phân thức khác mẫu để cộng (trừ) phân thức: Quy đồng mẫu thức rồi cộng (trừ) các phân thức cùng mẫu vừa tìm được
Lời giải chi tiết
Hình hộp chữ nhật có thể tích \(500c{m^3}\) có diện tích đáy là \(x\left( {x + 2} \right)\left( {c{m^2}} \right)\) và độ dài cạnh DF (cạnh AB) là: \(\frac{{500}}{{x\left( {x + 2} \right)}}\left( {cm} \right)\)
Hình hộp chữ nhật có thể tích \(200c{m^3}\) có diện tích đáy là \(x\left( {x + 1} \right)\left( {c{m^2}} \right)\) và độ dài cạnh EF (cạnh BC) là: \(\frac{{200}}{{x\left( {x + 1} \right)}}\left( {cm} \right)\)
Do đó, \(AC \) \(= AB + BC \) \(= \frac{{500}}{{x\left( {x + 2} \right)}} + \frac{{200}}{{x\left( {x + 1} \right)}} \) \(= \frac{{500\left( {x + 1} \right)}}{{x\left( {x + 1} \right)\left( {x + 2} \right)}} + \frac{{200\left( {x + 2} \right)}}{{x\left( {x + 1} \right)\left( {x + 2} \right)}}\)\(= \frac{{500x + 500 + 200x + 400}}{{x\left( {x + 1} \right)\left( {x + 2} \right)}} \) \(= \frac{{700x + 900}}{{x\left( {x + 1} \right)\left( {x + 2} \right)}}\left( {cm} \right)\)
\(DE \) \(= DF - EF \) \(= \frac{{500}}{{x\left( {x + 2} \right)}} - \frac{{200}}{{x\left( {x + 1} \right)}} \) \(= \frac{{500\left( {x + 1} \right)}}{{x\left( {x + 1} \right)\left( {x + 2} \right)}} - \frac{{200\left( {x + 2} \right)}}{{x\left( {x + 1} \right)\left( {x + 2} \right)}}\)\(= \frac{{500x + 500 - 200x - 400}}{{x\left( {x + 1} \right)\left( {x + 2} \right)}} \) \(= \frac{{300x + 100}}{{x\left( {x + 1} \right)\left( {x + 2} \right)}}\left( {cm} \right)\)
Bài 6.26 trang 10 sách bài tập Toán 8 Kết nối tri thức yêu cầu học sinh vận dụng kiến thức về các góc trong một tam giác, đặc biệt là tổng ba góc trong một tam giác bằng 180 độ, để giải quyết một bài toán thực tế liên quan đến việc đo đạc góc.
Cho hình vẽ, biết góc BAC = 40o, góc ABC = 60o. Tính góc ACB.
Trong tam giác ABC, ta có:
Vậy, góc ACB = 80o.
Bài toán này là một ứng dụng trực tiếp của định lý về tổng ba góc trong một tam giác. Để giải bài toán, chúng ta cần:
Ngoài bài 6.26, sách bài tập Toán 8 Kết nối tri thức còn có nhiều bài tập tương tự, yêu cầu học sinh vận dụng kiến thức về các góc trong một tam giác để giải quyết các bài toán khác nhau. Một số dạng bài tập thường gặp bao gồm:
Để giải các bài tập về góc trong tam giác một cách nhanh chóng và chính xác, bạn có thể áp dụng một số mẹo sau:
Kiến thức về góc trong tam giác có ứng dụng rất lớn trong thực tế, đặc biệt trong các lĩnh vực như:
Để củng cố kiến thức về góc trong tam giác, bạn có thể làm thêm một số bài tập sau:
Hy vọng với lời giải chi tiết và những hướng dẫn trên, các em học sinh sẽ hiểu rõ hơn về cách giải bài 6.26 trang 10 sách bài tập Toán 8 Kết nối tri thức và tự tin giải các bài tập tương tự.