Bài 9.55 trang 66 sách bài tập Toán 8 Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng giải bài toán thực tế liên quan đến ứng dụng của tam giác đồng dạng. Bài tập này thường yêu cầu học sinh vận dụng kiến thức về tỉ lệ thức, tam giác đồng dạng để tìm ra các đại lượng chưa biết.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 9.55 trang 66, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Lấy một điểm O nằm ngoài đoạn thẳng AB. Hãy vẽ hình đồng dạng phối cảnh của đoạn thẳng AB với tâm phối cảnh là điểm O và tỉ số đồng dạng bằng 2.
Đề bài
Lấy một điểm O nằm ngoài đoạn thẳng AB. Hãy vẽ hình đồng dạng phối cảnh của đoạn thẳng AB với tâm phối cảnh là điểm O và tỉ số đồng dạng bằng 2.
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức khái niệm hình đồng dạng phối cảnh để vẽ hình:
+ Cặp hình phóng to – thu nhỏ được gọi là các hình đồng dạng phối cảnh.
+ Nếu với mỗi điểm M thuộc hình \(\mathcal{K}\), lấy điểm M’ thuộc tia OM sao cho \(OM' = k.OM\) (hay \(\frac{{OM'}}{{OM}} = k\)) thì các điểm M’ đó tạo thành hình \(\mathcal{K}'\). Ta nói hình \(\mathcal{K}'\) đồng dạng phối cảnh với hình \(\mathcal{K}\) theo tỉ số đồng dạng (vị tự) k. Khi đó, điểm O là tâm phối cảnh.
Lời giải chi tiết
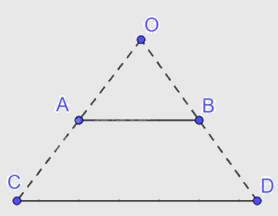
Trên tia OA, OB lần lượt lấy điểm C, D sao cho \(OC = 2OA,\;OD = 2OB.\) Nối C với D ta được đoạn thẳng CD là hình đồng dạng phối cảnh của đoạn thẳng AB với tâm phối cảnh là điểm O và tỉ số đồng dạng bằng 2.
Bài 9.55 trang 66 sách bài tập Toán 8 Kết nối tri thức yêu cầu học sinh giải quyết một bài toán thực tế liên quan đến việc tính chiều cao của một ngọn cây dựa vào bóng của cây và bóng của một người. Để giải bài toán này, chúng ta cần hiểu rõ về ứng dụng của tam giác đồng dạng trong việc giải quyết các bài toán thực tế.
Một ngọn cây cao 5m, người ta đo được bóng của cây trên mặt đất là 8m. Hỏi một người cao 1,6m có bóng trên mặt đất dài bao nhiêu mét?
Bài toán này có thể được giải quyết bằng cách sử dụng tính chất của tam giác đồng dạng. Chúng ta có thể hình dung bóng của cây và bóng của người tạo thành hai tam giác vuông đồng dạng. Tỉ lệ giữa chiều cao của cây và chiều dài bóng của cây sẽ bằng tỉ lệ giữa chiều cao của người và chiều dài bóng của người.
Gọi chiều dài bóng của người là x (m). Ta có tỉ lệ thức sau:
5/8 = 1.6/x
Giải phương trình trên, ta được:
x = (1.6 * 8) / 5 = 2.56
Vậy, bóng của người cao 1,6m trên mặt đất dài 2,56 mét.
Bước 1: Xác định các đại lượng đã biết và đại lượng cần tìm. Trong bài toán này, chúng ta đã biết chiều cao của cây (5m), chiều dài bóng của cây (8m) và chiều cao của người (1,6m). Chúng ta cần tìm chiều dài bóng của người.
Bước 2: Phân tích mối quan hệ giữa các đại lượng. Chúng ta nhận thấy rằng bóng của cây và bóng của người tạo thành hai tam giác vuông đồng dạng. Điều này có nghĩa là tỉ lệ giữa chiều cao của cây và chiều dài bóng của cây sẽ bằng tỉ lệ giữa chiều cao của người và chiều dài bóng của người.
Bước 3: Lập tỉ lệ thức và giải phương trình. Dựa vào mối quan hệ giữa các đại lượng, chúng ta lập tỉ lệ thức 5/8 = 1.6/x và giải phương trình để tìm ra giá trị của x.
Bước 4: Kiểm tra lại kết quả. Sau khi tìm được giá trị của x, chúng ta nên kiểm tra lại kết quả để đảm bảo rằng nó hợp lý và phù hợp với điều kiện của bài toán.
Ngoài bài 9.55, còn rất nhiều bài tập tương tự liên quan đến ứng dụng của tam giác đồng dạng trong việc giải quyết các bài toán thực tế. Một số dạng bài tập tương tự bao gồm:
Để giải các bài tập về tam giác đồng dạng một cách hiệu quả, bạn nên:
Bài 9.55 trang 66 sách bài tập Toán 8 Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng giải bài toán thực tế liên quan đến ứng dụng của tam giác đồng dạng. Hy vọng rằng với lời giải chi tiết và các hướng dẫn trên, các em học sinh sẽ nắm vững kiến thức và tự tin giải các bài tập tương tự.