Bài 8.15 trang 45 sách bài tập Toán 8 thuộc chương trình Kết nối tri thức với cuộc sống là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng áp dụng kiến thức về hình học đã học vào giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 8.15 này, giúp các em học sinh nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Trong tháng vừa qua có 3 084 người nhập cảnh ngắn hạn vào nước X. Cơ quan hải quan thống kê mục đích nhập cảnh của họ và cho kết quả trong bảng sau:
Đề bài
Trong tháng vừa qua có 3 084 người nhập cảnh ngắn hạn vào nước X. Cơ quan hải quan thống kê mục đích nhập cảnh của họ và cho kết quả trong bảng sau: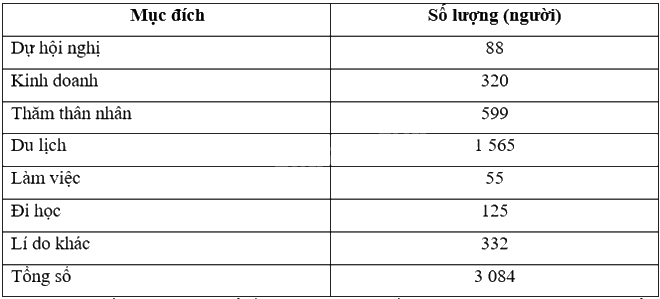
a) Tính xác suất thực nghiệm để người nhập cảnh ngắn hạn vào nước X tháng qua (biểu diễn bằng phần trăm) với mục đích:
b) Biết rằng tháng tới có 2 156 người nhập cảnh ngắn hạn vào nước X. Hãy dự đoán xem trong đó có:
Phương pháp giải - Xem chi tiết
+ Sử dụng kiến thức xác suất thực nghiệm của một biến cố để tính: Giả sử trong n lần thực nghiệm hoặc n lần theo dõi (quan sát) một hiện tượng ta thấy biến cố E xảy ra k lần. Khi đó xác suất thực nghiệm của biến cố E bằng \(\frac{k}{n}\), tức là bằng tỉ số giữa số lần xuất hiện biến cố E và số lần thực hiện thực nghiệm hoặc theo dõi hiện tượng đó.
+ Sử dụng mối liên hệ giữa xác suất thực nghiệm với xác suất: Xác suất của biến cố E được ước lượng bằng xác suất thực nghiệm của E: \(P\left( E \right) \approx \frac{k}{n};\)trong đó n là số lần thực nghiệm hay theo dõi một hiện tượng, k là số lần biến cố E xảy ra.
Lời giải chi tiết
a) Có 320 người nhập cảnh với mục đích kinh doanh nên xác suất thực nghiệm để người nhập cảnh ngắn hạn vào nước X tháng qua với mục đích kinh doanh là: \(\frac{{320}}{{3\;084}} \approx 10,38\% \)
Có 1 565 người nhập cảnh với mục đích du lịch nên xác suất thực nghiệm để người nhập cảnh ngắn hạn vào nước X tháng qua với mục đích du lịch là: \(\frac{{1\;565}}{{3\;084}} \approx 50,75\% \)
Có \(55 + 125 = 180\) người nhập cảnh với mục đích làm việc hoặc đi học nên xác suất thực nghiệm để người nhập cảnh ngắn hạn vào nước X tháng qua với mục đích làm việc hoặc đi học là: \(\frac{{180}}{{3\;084}} \approx 5,84\% \)
Có \(88 + 320 = 408\) người nhập cảnh với mục đích kinh doanh hoặc dự hội nghị nên xác suất thực nghiệm để người nhập cảnh ngắn hạn vào nước X tháng qua với mục đích kinh doanh hoặc dự hội nghị là: \(\frac{{408}}{{3\;084}} \approx 13,23\% \)
b) Gọi k là số người nhập cảnh với mục đích du lịch trong tháng sau.
Ta có: \(\frac{k}{{2\;156}} \approx \frac{{1\;565}}{{3\;084}}\) nên \(k \approx \frac{{2\;156.1\;565}}{{3\;084}} \approx 1\;094,08\)
Do đó, ta dự đoán trong tháng sau có khoảng 1 094 người nhập cảnh ngắn hạn vào nước X với mục đích du lịch.
Gọi h là số người nhập cảnh với mục đích kinh doanh, làm việc hoặc đi học trong tháng sau.
Ta có: \(\frac{h}{{2\;156}} \approx \frac{{320 + 55 + 125}}{{3\;084}} = \frac{{500}}{{3\;084}}\) nên \(h \approx \frac{{2\;156.500}}{{3\;084}} \approx 349,55\)
Do đó, ta dự đoán trong tháng sau có khoảng 350 người nhập cảnh với mục đích kinh doanh, làm việc hoặc đi học.
Bài 8.15 yêu cầu chúng ta xét hình thang cân ABCD (AB // CD, AD = BC) và tìm mối quan hệ giữa các góc. Để giải bài toán này, chúng ta cần nắm vững các tính chất của hình thang cân, đặc biệt là tính chất về các góc kề một cạnh bên và tổng hai góc kề một đáy.
Đề bài cho hình thang cân ABCD với AB // CD và AD = BC. Yêu cầu là tìm mối quan hệ giữa các góc. Để giải quyết bài toán này, chúng ta cần:
Chứng minh:
Để hiểu rõ hơn về tính chất này, chúng ta có thể xét một ví dụ cụ thể. Giả sử ∠A = 60°, khi đó ∠B = 60° và ∠D = 120°, ∠C = 120°. Như vậy, tổng hai góc kề một đáy luôn bằng 180°.
Bài tập tương tự:
Cho hình thang cân MNPQ (MN // PQ, MP = NQ). Tính tổng các góc của hình thang cân.
Hướng dẫn: Sử dụng tính chất tổng các góc trong một tứ giác bằng 360° và các tính chất của hình thang cân để giải bài toán.
Kiến thức về hình thang cân và các tính chất của nó có ứng dụng rộng rãi trong thực tế, đặc biệt trong các lĩnh vực như kiến trúc, xây dựng, và thiết kế. Ví dụ, trong kiến trúc, hình thang cân thường được sử dụng trong thiết kế mái nhà, cửa sổ, và các chi tiết trang trí khác.
Bài 8.15 trang 45 sách bài tập Toán 8 - Kết nối tri thức là một bài tập quan trọng giúp học sinh củng cố kiến thức về hình thang cân. Hy vọng với lời giải chi tiết và các ví dụ minh họa trên, các em học sinh sẽ hiểu rõ hơn về bài toán này và tự tin hơn trong quá trình học tập môn Toán.
Giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán. Hãy truy cập website của chúng tôi để tìm hiểu thêm nhiều bài giải và tài liệu học tập hữu ích khác.