Bài 10.16 trang 79 sách bài tập Toán 8 - Kết Nối Tri Thức là một bài tập quan trọng trong chương trình học Toán 8. Bài tập này yêu cầu học sinh vận dụng kiến thức về các định lý đã học để giải quyết các bài toán thực tế.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho bài 10.16 này, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
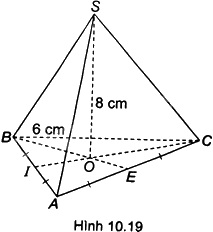
Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng 6cm, chiều cao 8cm như Hình 10.19.
Đề bài
Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng 6cm, chiều cao 8cm như Hình 10.19. Tính thể tích hình chóp, biết \(\sqrt {27} \approx 5,2\)
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức về thể tích của hình chóp tam giác đều: Thể tích của hình chóp tam giác đều bằng \(\frac{1}{3}\) tích của diện tích đáy với chiều cao của nó.
Lời giải chi tiết
Kẻ các đường cao IC, BE của tam giác đều ABC. Gọi O là giao điểm của BE và IC, khi đó SO là đường cao của hình chóp tam giác đều S.ABC.
Tam giác ABC là tam giác đều nên \(AB = BC = 6cm\), CI là đường cao đồng thời là đường trung tuyến. Do đó, \(BI = \frac{1}{2}AB = 3cm\).
Áp dụng định lí Pythagore vào tam giác CBI vuông tại I có: \(B{I^2} + I{C^2} = B{C^2}\)
\(I{C^2} = B{C^2} - B{I^2} = {6^2} - {3^2} = 27\) nên \(BI = \sqrt {27} \approx 5,2cm\)
Diện tích tam giác ABC là: \(S = \frac{1}{2}IC.AB \approx \frac{1}{2}.5,2.6 = 15,6\left( {c{m^2}} \right)\)
Thể tích hình chóp là: \(V = \frac{1}{3}.15,6.8 = 41,6\left( {c{m^3}} \right)\)
Bài 10.16 trang 79 sách bài tập Toán 8 - Kết Nối Tri Thức yêu cầu chúng ta giải quyết một bài toán liên quan đến hình học, cụ thể là việc chứng minh các tính chất của hình thang cân. Để giải bài toán này một cách hiệu quả, chúng ta cần nắm vững các kiến thức cơ bản về hình thang cân, bao gồm:
Đề bài: (Giả sử đề bài là: Cho hình thang cân ABCD (AB // CD). Gọi E là giao điểm của AC và BD. Chứng minh rằng EA = EB.)
Lời giải:
Do đó, ΔADC = ΔBCD (c-g-c)
Giải thích chi tiết:
Bước 1: Chúng ta bắt đầu bằng việc xác định các yếu tố cần thiết để chứng minh hai tam giác bằng nhau. Trong trường hợp này, chúng ta cần chứng minh ΔADC và ΔBCD bằng nhau.
Bước 2: Chúng ta sử dụng các tính chất của hình thang cân để xác định các cạnh và góc bằng nhau. Cụ thể, chúng ta biết rằng AC = BD (tính chất hình thang cân) và DC là cạnh chung của hai tam giác.
Bước 3: Chúng ta sử dụng tính chất của các đường thẳng song song để xác định các góc bằng nhau. Trong trường hợp này, chúng ta biết rằng ∠ACD = ∠BDC (so le trong do AB // CD).
Bước 4: Chúng ta sử dụng tiêu chuẩn bằng nhau cạnh - góc - cạnh (c-g-c) để chứng minh hai tam giác bằng nhau. Vì chúng ta đã xác định được hai cạnh và một góc bằng nhau, chúng ta có thể kết luận rằng ΔADC = ΔBCD.
Bước 5: Cuối cùng, chúng ta sử dụng tính chất của hai tam giác bằng nhau để suy ra rằng EA = EB (cạnh tương ứng).
Ngoài bài toán chứng minh tính chất của hình thang cân, còn rất nhiều dạng bài tập tương tự khác. Một số dạng bài tập phổ biến bao gồm:
Để giải các bài tập này, chúng ta cần nắm vững các kiến thức cơ bản về hình học, bao gồm:
Ngoài ra, chúng ta cũng cần rèn luyện kỹ năng giải toán và tư duy logic để có thể giải quyết các bài toán một cách hiệu quả.
Để củng cố kiến thức và kỹ năng giải toán, bạn có thể luyện tập thêm các bài tập sau:
Kết luận:
Bài 10.16 trang 79 sách bài tập Toán 8 - Kết Nối Tri Thức là một bài tập quan trọng giúp học sinh củng cố kiến thức về hình thang cân. Bằng cách nắm vững các kiến thức cơ bản và rèn luyện kỹ năng giải toán, các em học sinh có thể tự tin giải quyết các bài toán tương tự.