Bài 9.39 trang 60 Sách bài tập Toán 8 - Kết nối tri thức là một bài tập quan trọng trong chương trình học Toán 8. Bài tập này yêu cầu học sinh vận dụng kiến thức về hình học, cụ thể là các tính chất của hình thang cân để giải quyết vấn đề.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 9.39 trang 60 Sách bài tập Toán 8 - Kết nối tri thức, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Tính diện tích của một tam giác cân, biết rằng tam giác đó có hai cạnh với độ dài bằng 4cm và 8cm.
Đề bài
Tính diện tích của một tam giác cân, biết rằng tam giác đó có hai cạnh với độ dài bằng 4cm và 8cm.
Phương pháp giải - Xem chi tiết
+ Sử dụng kiến thức định lí Pythagore để tính độ dài đường cao: Trong một tam giác vuông, bình phương cạnh huyền bằng tổng các bình phương của hai cạnh góc vuông.
+ Sử dụng tính chất tam giác cân: Trong tam giác cân, đường cao xuất phát từ đỉnh đồng thời là đường trung tuyến.
+ Sử dụng công thức tính diện tích tam giác để tính diện tích tam giác: Diện tích tam giác bằng nửa tích chiều cao nhân với đáy (chiều cao là chiều cao ứng với đáy đó).
Lời giải chi tiết
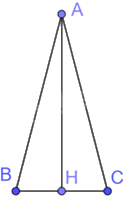
Vì tam giác cân có hai cạnh là 4cm và 8cm nên độ dài ba cạnh của tam giác đó là 4cm, 8cm, 8cm.
Giả sử tam giác ABC cân tại A có \(AB = AC = 8cm,BC = 4cm\)
Kẻ đường cao AH (H thuộc BC) của tam giác ABC cân tại A. Khi đó, H là trung điểm của BC nên \(BH = \frac{1}{2}BC = 2cm\)
Áp dụng định lí Pythagore vào tam giác ABH vuông tại H có:
\(A{H^2} + B{H^2} = A{B^2}\)
\(A{H^2} = A{B^2} - B{H^2} = {8^2} - {2^2} = 60\)
Do đó, \(AH = 2\sqrt {15} cm\)
Diện tích tam giác ABC là: \(\frac{1}{2}AH.BC = \frac{1}{2}.2\sqrt {15} .4 = 4\sqrt {15} \left( {c{m^2}} \right)\)
Bài 9.39 trang 60 Sách bài tập Toán 8 - Kết nối tri thức yêu cầu chúng ta giải quyết một bài toán liên quan đến hình thang cân. Để giải bài toán này một cách hiệu quả, chúng ta cần nắm vững các kiến thức cơ bản về hình thang cân, bao gồm:
Đề bài: (Giả sử đề bài là: Cho hình thang cân ABCD (AB // CD), có AB = 5cm, CD = 10cm, AD = BC = 6cm. Tính chiều cao của hình thang.)
Lời giải:
Kết luận: Chiều cao của hình thang ABCD là khoảng 5.45cm.
Ngoài bài toán tính chiều cao, bài tập về hình thang cân còn có nhiều dạng khác như:
Để giải các bài tập này, chúng ta cần:
Để củng cố kiến thức và kỹ năng giải bài tập về hình thang cân, các em học sinh nên luyện tập thêm các bài tập tương tự trong sách bài tập và các đề thi thử. Giaitoan.edu.vn sẽ cung cấp thêm nhiều bài tập và lời giải chi tiết trong các bài viết tiếp theo.
Bài 9.39 trang 60 Sách bài tập Toán 8 - Kết nối tri thức là một bài tập điển hình về hình thang cân. Việc nắm vững kiến thức và kỹ năng giải bài tập này sẽ giúp các em học sinh tự tin hơn trong việc học Toán 8. Hy vọng với lời giải chi tiết và hướng dẫn cụ thể trên đây, các em sẽ hiểu rõ hơn về bài toán và có thể tự giải các bài tập tương tự.