Bài 5.19 trang 71 sách bài tập Toán 8 thuộc chương trình Kết nối tri thức với cuộc sống là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng áp dụng kiến thức về hình học đã học vào giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 5.19 này, giúp các em học sinh nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Biểu đồ Hình 5.12, cho biết số bàn thắng ghi được của chủ nhân chiếc giày vàng tại giải ngoại hạng Anh và La Liga
Đề bài
Biểu đồ Hình 5.12, cho biết số bàn thắng ghi được của chủ nhân chiếc giày vàng tại giải ngoại hạng Anh và La Liga (giải vô địch quốc gia Tây Ban Nha trong một số năm gần đây.
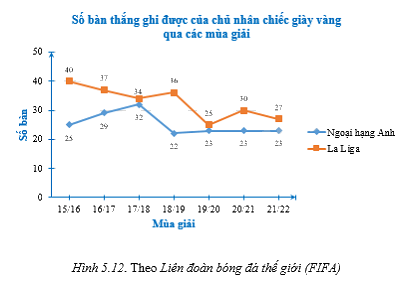
a) So sánh về số bàn thắng mà chủ nhân chiếc giày vàng ghi được tại hai giải bóng đá từ mùa giải 2015/2016 đến mùa giải 2021/2022.
b) Cầu thủ ghi được nhiều nhất bao nhiêu bàn thắng trong một mùa giải tính từ mùa giải 2015/2016 đến mùa giải 2021/2022?
Phương pháp giải - Xem chi tiết
Quan sát biểu đồ rồi so sánh về số bàn thắng mà chủ nhân chiếc giày vàng ghi được tại hai giải bóng đá, xem số bàn thắng ghi được nhiều nhất.
Lời giải chi tiết
a) Từ mùa giải 2015/2016 đến mùa giải 2021/2022, cầu thủ đoạt danh hiệu chiếc giày vàng ở giải La Liga luôn ghi nhiều bàn thắng hơn cầu thủ đoạt danh hiệu chiếc giày vàng ở giải ngoại hạng Anh.
b) Cầu thủ ghi được nhiều nhất 40 bàn thắng (chủ nhân chiếc giày vàng tại giải La Liga mùa giải 2015/2016) trong một mùa giải tính từ mùa giải 2015/2016 đến mùa giải 2021/2022.
Bài 5.19 yêu cầu chúng ta xét hình thang cân ABCD (AB // CD, AD = BC) và điểm E nằm trên cạnh AB sao cho AE = EB. Chúng ta cần chứng minh rằng DE = EC. Bài toán này đòi hỏi sự hiểu biết về các tính chất của hình thang cân, đặc biệt là sự đối xứng của nó.
Đề bài cho hình thang cân ABCD, với AB song song CD và AD bằng BC. Điểm E nằm trên AB sao cho AE bằng EB. Yêu cầu chứng minh DE bằng EC. Hướng giải chính là sử dụng các tính chất của hình thang cân để chứng minh hai tam giác ADE và BCE bằng nhau theo trường hợp cạnh - góc - cạnh (c-g-c).
a) Chứng minh tam giác ADE và BCE bằng nhau:
b) Suy ra DE = EC:
Vì tam giác ADE bằng tam giác BCE (chứng minh trên), nên DE = EC (hai cạnh tương ứng).
Hình thang cân là một hình thang đặc biệt, có hai cạnh đáy song song và hai cạnh bên bằng nhau. Một trong những tính chất quan trọng nhất của hình thang cân là hai góc đáy bằng nhau. Tính chất này đóng vai trò then chốt trong việc chứng minh hai tam giác ADE và BCE bằng nhau trong bài toán này.
Để hiểu sâu hơn về hình thang cân và các tính chất của nó, các em có thể làm thêm các bài tập tương tự. Ví dụ:
Khi giải các bài tập hình học, các em nên:
Kiến thức về hình thang cân có ứng dụng rộng rãi trong thực tế, ví dụ như trong kiến trúc, xây dựng, thiết kế các vật dụng hàng ngày. Việc hiểu rõ về hình thang cân giúp chúng ta giải quyết các vấn đề thực tế một cách hiệu quả hơn.
Bài 5.19 trang 71 sách bài tập Toán 8 - Kết nối tri thức với cuộc sống là một bài tập điển hình về hình thang cân. Việc nắm vững các tính chất của hình thang cân và áp dụng chúng một cách linh hoạt sẽ giúp các em giải quyết bài toán này một cách dễ dàng. Hy vọng với lời giải chi tiết và hướng dẫn trên, các em sẽ hiểu rõ hơn về bài toán này và tự tin hơn trong quá trình học tập môn Toán.
| Khái niệm | Định nghĩa |
|---|---|
| Hình thang cân | Hình thang có hai cạnh bên bằng nhau. |
| Góc đáy | Hai góc kề với một cạnh đáy của hình thang cân. |