Bài 3.22 trang 39 sách bài tập Toán 8 Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng giải bài toán thực tế liên quan đến các ứng dụng của tam giác đồng dạng. Bài tập này thường yêu cầu học sinh vận dụng kiến thức về tỉ lệ thức, tam giác đồng dạng để giải quyết các vấn đề về chiều cao, khoảng cách.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 3.22 trang 39 sách bài tập Toán 8 Kết nối tri thức, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
1. Sử dụng tính chất tổng các góc của một tam giác bằng \({180^0}\) để chứng minh:
Đề bài
1. Sử dụng tính chất tổng các góc của một tam giác bằng \({180^0}\) để chứng minh:
a) Trong một tam giác vuông, đường trung tuyến ứng với cạnh huyền bằng nửa cạnh huyền.
b) Tam giác ABC có đường trung tuyến AM bằng nửa BC thì tam giác vuông tại A.
2. Sử dụng tính chất hai đường chéo của hình chữ nhật bằng nhau để chứng minh a), b) của ý 1.
Phương pháp giải - Xem chi tiết
2a: Sử dụng kiến thức về tính chất hình chữ nhật để chứng minh: Hình chữ nhật có hai đường chéo bằng nhau và cắt nhau tại trung điểm mỗi đường.
2b: Sử dụng kiến thức về dấu hiệu nhận biết hình chữ nhật để chứng minh: Hình bình hành có hai đường chéo bằng nhau là hình chữ nhật.
Lời giải chi tiết
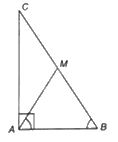
1.
a) Giả sử tam giác ABC vuông tại A.
Do B là góc nhọn, lấy điểm M thuộc BC sao cho \(\widehat {BAM} = \widehat {ABM}\) nên tam giác ABM cân tại M. Do đó, \(AM = MB\)
Vì \(\widehat {BAM} + \widehat {MAC} = \widehat {ABM} + \widehat {ACM} = {90^0}\) nên \(\widehat {MAC} = \widehat {ACM}\), do đó, tam giác AMC cân tại M. Do đó, \(MA = MC.\)
Vậy \(MA = MB = MC = \frac{1}{2}BC\)
b) Ngược lại, nếu M thuộc BC sao cho \(MA = MB = MC = \frac{1}{2}BC\) thì tam giác MAB cân tại M, tam giác MAC cân tại M.
Suy ra, \(\widehat {MAB} = \widehat B,\widehat {MAC} = \widehat C\)
Ta có: \(\widehat {BAC} = \widehat {MAC} + \widehat {MAB}\)
Nên \(\widehat {BAC} = \widehat B + \widehat C\), mà \(\widehat {BAC} + \widehat B + \widehat C = {180^0}\) nên \(\widehat {BAC} = {90^0}\)
Do đó, tam giác ABC vuông tại A.
2.
Gọi M là trung điểm của BC, lấy điểm P sao cho M là trung điểm của AP thì tứ giác ABPC là hình bình hành.
a) Nếu tam giác ABC vuông tại A thì hình bình hành ABPC có \(\widehat {BAC} = {90^0}\) nên ABPC là hình chữ nhật. Do hai đường chéo AP, BC bằng nhau nên \(MA = MB = MC = MP\)
b) Nếu M thuộc BC sao cho \(MA = MB = MC = \frac{1}{2}BC\) thì suy ra \(BC = AP\). Khi đó, hình bình hành ABPC có hai đường chéo bằng nhau nên ABPC là hình chữ nhật. Do đó, \(\widehat {CAB} = {90^0}\)
Vậy tam giác ABC vuông tại A.
Bài 3.22 trang 39 sách bài tập Toán 8 Kết nối tri thức yêu cầu học sinh giải quyết một bài toán thực tế liên quan đến việc tính chiều cao của một vật thể dựa trên bóng của nó và góc tạo bởi tia nắng mặt trời. Để giải bài toán này, học sinh cần nắm vững kiến thức về tam giác đồng dạng và các tính chất liên quan đến tỉ lệ thức.
Trước khi đi vào giải bài toán, chúng ta cần phân tích đề bài để xác định các yếu tố quan trọng. Trong bài toán này, chúng ta có một vật thể (ví dụ: cột điện, cây cối) và bóng của nó trên mặt đất. Góc tạo bởi tia nắng mặt trời và mặt đất là một yếu tố quan trọng để xác định mối quan hệ giữa chiều cao của vật thể và chiều dài bóng của nó.
Để giải bài toán, chúng ta có thể sử dụng kiến thức về tam giác đồng dạng. Nếu chúng ta coi vật thể và bóng của nó tạo thành một tam giác vuông, thì chúng ta có thể tìm ra một tam giác đồng dạng khác có tỉ lệ tương ứng. Từ đó, chúng ta có thể sử dụng tỉ lệ thức để tính chiều cao của vật thể.
Giả sử chúng ta có một cột điện cao 6 mét và bóng của nó trên mặt đất dài 8 mét. Góc tạo bởi tia nắng mặt trời và mặt đất là 30 độ. Chúng ta có thể sử dụng kiến thức về tam giác đồng dạng để tính chiều cao của cột điện.
Trong trường hợp này, chúng ta có thể coi cột điện và bóng của nó tạo thành một tam giác vuông. Chúng ta cũng có thể tìm ra một tam giác đồng dạng khác có tỉ lệ tương ứng. Từ đó, chúng ta có thể sử dụng tỉ lệ thức để tính chiều cao của cột điện.
Để rèn luyện kỹ năng giải bài toán về tam giác đồng dạng, bạn có thể làm thêm các bài tập tương tự trong sách bài tập Toán 8 Kết nối tri thức. Ngoài ra, bạn cũng có thể tìm kiếm các bài tập trực tuyến trên các trang web học toán.
Bài 3.22 trang 39 sách bài tập Toán 8 Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng giải bài toán thực tế liên quan đến tam giác đồng dạng. Bằng cách nắm vững kiến thức về tam giác đồng dạng và áp dụng các bước giải bài toán một cách chính xác, học sinh có thể tự tin giải quyết các bài tập tương tự.
| Công thức | Mô tả |
|---|---|
| Tỉ lệ thức | a/b = c/d |
| Tam giác đồng dạng | Hai tam giác có các góc tương ứng bằng nhau thì đồng dạng. |