Bài 4.17 trang 55 sách bài tập Toán 8 Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng giải bài toán thực tế liên quan đến các góc trong tam giác. Bài tập này yêu cầu học sinh vận dụng kiến thức về tổng ba góc trong một tam giác để tìm ra các góc chưa biết.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 4.17 trang 55, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Cho tam giác ABC cân tại A, các đường phân giác BD, CE \(\left( {D \in AC,E \in AB} \right)\). Chứng minh DE//BC
Đề bài
Cho tam giác ABC cân tại A, các đường phân giác BD, CE \(\left( {D \in AC,E \in AB} \right)\). Chứng minh DE//BC
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức về tính chất đường phân giác của tam giác để chứng minh: Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề với hai đoạn thẳng ấy.
Lời giải chi tiết
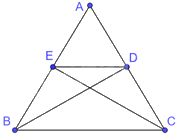
Tam giác ABC cân tại A nên \(AB = AC\)
Vì CE là phân giác của góc ACB trong tam giác ABC nên \(\frac{{AE}}{{BE}} = \frac{{AC}}{{BC}}\) (tính chất đường phân giác của tam giác)
Vì BD là phân giác của góc ABC trong tam giác ABC nên \(\frac{{AD}}{{DC}} = \frac{{AB}}{{BC}}\) (tính chất đường phân giác của tam giác)
Do đó, \(\frac{{AE}}{{BE}} = \frac{{AD}}{{DC}}\)
Tam giác ABC có: \(\frac{{AE}}{{BE}} = \frac{{AD}}{{DC}}\) nên ED//BC (định lí Thalès đảo)
Bài 4.17 trang 55 sách bài tập Toán 8 Kết nối tri thức yêu cầu chúng ta giải quyết một bài toán thực tế liên quan đến việc tính toán các góc trong một tam giác. Để giải bài toán này, chúng ta cần nắm vững kiến thức về tổng ba góc trong một tam giác, đó là 180 độ.
Cho hình vẽ, biết góc BAC = 30° và góc ABC = 70°. Tính số đo góc ACB.
Trong tam giác ABC, ta có:
∠BAC + ∠ABC + ∠ACB = 180° (Tổng ba góc trong một tam giác)
Thay số:
30° + 70° + ∠ACB = 180°
100° + ∠ACB = 180°
∠ACB = 180° - 100°
∠ACB = 80°
Vậy, số đo góc ACB là 80°.
Để giải bài toán này, chúng ta đã sử dụng tính chất cơ bản của tam giác, đó là tổng ba góc trong một tam giác luôn bằng 180 độ. Bằng cách thay các giá trị góc đã biết vào công thức, chúng ta có thể dễ dàng tính toán được góc còn lại.
Các bài tập tương tự bài 4.17 thường yêu cầu chúng ta tính toán các góc trong tam giác dựa trên các thông tin đã cho. Các bài tập này có thể có nhiều dạng khác nhau, ví dụ như:
Để giải các bài tập về góc trong tam giác một cách hiệu quả, bạn nên:
Ví dụ 1: Cho tam giác DEF có ∠D = 60° và ∠E = 50°. Tính ∠F.
Lời giải:
∠D + ∠E + ∠F = 180°
60° + 50° + ∠F = 180°
∠F = 180° - 110°
∠F = 70°
Ví dụ 2: Cho tam giác GHI có ∠G = 90° và ∠H = 45°. Tính ∠I.
Lời giải:
∠G + ∠H + ∠I = 180°
90° + 45° + ∠I = 180°
∠I = 180° - 135°
∠I = 45°
Bài 4.17 trang 55 sách bài tập Toán 8 Kết nối tri thức là một bài tập cơ bản nhưng quan trọng, giúp học sinh củng cố kiến thức về góc trong tam giác. Hy vọng với lời giải chi tiết và các ví dụ minh họa trên, các em học sinh sẽ hiểu rõ hơn về bài toán và tự tin giải các bài tập tương tự.
| Góc | Số đo |
|---|---|
| ∠BAC | 30° |
| ∠ABC | 70° |
| ∠ACB | 80° |