Bài 7.49 trang 37 sách bài tập Toán 8 Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng giải bài toán thực tế liên quan đến các ứng dụng của tam giác đồng dạng. Bài tập này thường yêu cầu học sinh vận dụng kiến thức về tỉ lệ thức, tam giác đồng dạng để giải quyết các vấn đề về chiều cao, khoảng cách.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 7.49 trang 37, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Chị Lan vay mẹ 900 nghìn đồng và dự định trả cho mẹ 100 nghìn đồng mỗi tuần.
Đề bài
Chị Lan vay mẹ 900 nghìn đồng và dự định trả cho mẹ 100 nghìn đồng mỗi tuần.
a) Viết công thức của hàm số biểu thị số tiền y (nghìn đồng) mà chị Lan còn nợ mẹ sau x (tuần) vay.
b) Vẽ đồ thị của hàm số thu được ở câu a. Từ đó tìm số tiền mà chị Lan nợ mẹ sau 4 tuần.
c) Giao điểm của đồ thị với trục hoành biểu thị điều gì?
Phương pháp giải - Xem chi tiết
a) Sử dụng khái niệm hàm số bậc nhất: Hàm số bậc nhất là hàm số cho bởi công thức \(y = ax + b,\) trong đó a, b là các số cho trước và \(a \ne 0\).
b) Sử dụng kiến thức về cách vẽ đồ thị hàm số bậc nhất \(y = ax + b\left( {a \ne 0} \right)\) để vẽ đồ thị
+ Khi \(b = 0\) thì \(y = ax\). Đồ thị của hàm số \(y = ax\) là đường thẳng đi qua gốc tọa độ O(0; 0) và điểm A(1; a)
+ Khi \(b \ne 0\), ta thường xác định hai điểm đặc biệt trên đồ thị là giao điểm của đồ thị với hai trục tọa độ như sau:
- Cho \(x = 0\) thì \(y = b\), ta được điểm P(0; b) thuộc trục tung Oy.
- Cho \(y = 0\) thì \(x = \frac{{ - b}}{a}\), ta được điểm \(Q\left( { - \frac{b}{a};0} \right)\) thuộc trục hoành Ox.
- Vẽ đường thẳng đi qua hai điểm P, Q ta được đồ thị của hàm số \(y = ax + b\)
Lời giải chi tiết
a) Số tiền chị Lan trả cho mẹ trong x tuần là: \(100x\) (nghìn đồng)
Công thức của hàm số biểu thị số tiền y (nghìn đồng) mà chị Lan còn nợ mẹ sau x (tuần) vay là: \(y = 900 - 100x\) (nghìn đồng)
b) Đồ thị hàm số: \(y = 900 - 100x\) (nghìn đồng) đi qua hai điểm B(0; 900) và G(9; 0)
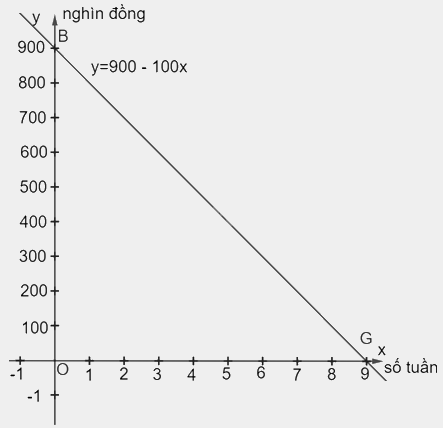
Với \(x = 4\) ta có: \(y = 900 - 100.4 = 500\) (nghìn đồng)
Vậy số tiền mà chị Lan nợ mẹ sau 4 tuần là 500 nghìn đồng.
c) Giao điểm của đồ thị hàm số \(y = 900 - 100x\) với trục hoành là điểm (9; 0). Giao điểm này biểu thị số tuần cần thiết để chị Lan trả hết nợ cho mẹ.
Bài 7.49 trang 37 sách bài tập Toán 8 Kết nối tri thức yêu cầu học sinh giải quyết một bài toán thực tế liên quan đến việc tính chiều cao của một vật thể dựa trên bóng của nó và góc tạo bởi tia nắng mặt trời. Để giải bài toán này, chúng ta cần hiểu rõ về ứng dụng của tam giác đồng dạng trong việc tính toán các đại lượng liên quan đến hình học.
Một người đứng ở vị trí A cách một cột điện 15m. Chiều cao của người đó là 1,6m. Người đó quan sát thấy bóng của cột điện trên mặt đất dài 20m. Tính chiều cao của cột điện.
Bài toán này có thể được giải bằng cách sử dụng tính chất của tam giác đồng dạng. Ta có thể hình dung cột điện và bóng của nó tạo thành một tam giác vuông, và người quan sát cùng bóng của mình cũng tạo thành một tam giác vuông. Hai tam giác này đồng dạng với nhau, do đó ta có thể thiết lập tỉ lệ thức để tìm chiều cao của cột điện.
Gọi chiều cao của cột điện là h (m). Ta có hai tam giác đồng dạng: tam giác tạo bởi cột điện và bóng của nó, và tam giác tạo bởi người quan sát và bóng của người đó.
Áp dụng tính chất của tam giác đồng dạng, ta có:
h / 20 = 1.6 / (20 - 15)
h / 20 = 1.6 / 5
h = (1.6 * 20) / 5
h = 6.4
Vậy chiều cao của cột điện là 6.4m.
Ứng dụng của tam giác đồng dạng không chỉ giới hạn trong việc giải các bài toán về chiều cao và khoảng cách. Nó còn được sử dụng trong nhiều lĩnh vực khác như đo đạc bản đồ, xây dựng công trình, và trong các bài toán liên quan đến hình học không gian.
Để củng cố kiến thức về tam giác đồng dạng và ứng dụng của nó, bạn có thể giải thêm các bài tập sau:
Bài 7.49 trang 37 sách bài tập Toán 8 Kết nối tri thức là một bài tập điển hình để rèn luyện kỹ năng giải bài toán thực tế bằng cách sử dụng tính chất của tam giác đồng dạng. Hy vọng rằng với lời giải chi tiết và hướng dẫn cụ thể trên đây, các em học sinh sẽ nắm vững kiến thức và tự tin giải các bài tập tương tự.
| Đại lượng | Giá trị |
|---|---|
| Khoảng cách từ người đến cột điện | 15m |
| Chiều cao của người | 1.6m |
| Chiều dài bóng của cột điện | 20m |
| Chiều cao của cột điện | 6.4m |
| Bảng tổng hợp các đại lượng trong bài toán | |