Bài 3.18 trang 37 sách bài tập Toán 8 thuộc chương trình Kết nối tri thức với cuộc sống là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng áp dụng kiến thức về các góc tạo bởi đường thẳng cắt đường thẳng. Bài tập này thường yêu cầu học sinh phải phân tích hình vẽ, xác định các góc so le trong, đồng vị, và sử dụng các tính chất của chúng để tìm ra các góc chưa biết.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 3.18 trang 37, giúp các em học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
Cho hình bình hành ABCD. Lấy các điểm E thuộc AB, F thuộc CD sao cho (AE = CF); lấy các điểm G thuộc BC, H thuộc AD sao cho (BG = DH.)
Đề bài
Cho hình bình hành ABCD. Lấy các điểm E thuộc AB, F thuộc CD sao cho \(AE = CF\); lấy các điểm G thuộc BC, H thuộc AD sao cho \(BG = DH.\) Chứng minh EGFH là một hình bình hành và các đường thẳng AC, BD, EF, GH đồng quy.
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức về tính chất hình bình hành để chứng minh: Hình bình hành có:
+ Các cạnh đối bằng nhau và song song.
+ Các góc đối bằng nhau.
+ Hai đường chéo cắt nhau tại trung điểm của mỗi đường.
Lời giải chi tiết
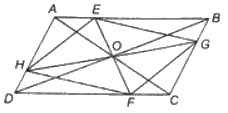
Vì ABCD là hình bình hành nên \(AB = CD,AD = BC,\) \(\widehat {ABC} = \widehat {ADC},\widehat {DAB} = \widehat {DCB}\)
Vì \(AB = CD\), \(AE = CF\) nên \(AB - AE = CD - FC\), suy ra \(EB = DF\)
Vì \(AD = BC\), \(DH = BG\) nên \(AD - DH = BC - BG\), suy ra \(AH = CG\)
Tam giác HEA và tam giác GCF có:
\(AE = CF\left( {gt} \right),\widehat {HAE} = \widehat {GCF}\left( {cmt} \right),AH = CG\left( {cmt} \right)\)
Do đó, \(\Delta HAE = \Delta GCF\left( {c - g - c} \right)\), suy ra \(HE = FG\)
Tam giác EBG và tam giác FDH có:
\(BG = DH\left( {gt} \right),\widehat {EBG} = \widehat {HDF}\left( {cmt} \right),EB = DF\left( {cmt} \right)\)
Do đó, \(\Delta EBG = \Delta FDH\left( {c - g - c} \right)\), suy ra \(GE = FH\)
Tứ giác EGFH có: \(HE = FG\), \(GE = FH\) nên EGFH là một hình bình hành.
Gọi O là trung điểm của AC.
Vì ABCD là hình bình hành nên hai đường chéo AC, BD cắt nhau tại O và O là trung điểm của BD (1).
Tứ giác EBFD có: EB//DF, \(EB = DF\) nên tứ giác EBDF là hình bình hành. Do đó, hai đường chéo EF và BD cắt nhau tại trung điểm O của BD (2).
Vì tứ giác EGFH là hình bình hành nên hai đường chéo EF và GH cắt nhau tại trung điểm O của EF (3).
Từ (1), (2) và (3) ta có: Các đường thẳng AC, BD, EF, GH đồng quy tại O.
Bài 3.18 trang 37 sách bài tập Toán 8 - Kết nối tri thức với cuộc sống yêu cầu học sinh vận dụng kiến thức về các góc tạo bởi đường thẳng cắt đường thẳng để giải quyết các bài toán thực tế. Dưới đây là hướng dẫn chi tiết cách giải bài tập này:
Trước khi bắt đầu giải bài tập, học sinh cần đọc kỹ đề bài, xác định rõ yêu cầu của bài toán. Điều này giúp học sinh tập trung vào việc tìm kiếm thông tin cần thiết và lựa chọn phương pháp giải phù hợp.
Để giải bài 3.18 trang 37, học sinh cần nắm vững các kiến thức sau:
(Nội dung lời giải chi tiết bài 3.18 trang 37 sẽ được trình bày tại đây, bao gồm hình vẽ minh họa, các bước giải cụ thể, và giải thích rõ ràng từng bước. Ví dụ:)
Ví dụ: Giả sử đề bài yêu cầu tìm số đo góc x trong hình vẽ, biết góc y = 60 độ. Ta có thể sử dụng tính chất hai góc so le trong bằng nhau để suy ra x = y = 60 độ.
Ngoài bài 3.18 trang 37, còn rất nhiều bài tập tương tự yêu cầu học sinh vận dụng kiến thức về các góc tạo bởi đường thẳng cắt đường thẳng. Để giải quyết các bài tập này, học sinh có thể áp dụng các phương pháp sau:
Để củng cố kiến thức và rèn luyện kỹ năng giải bài tập, học sinh có thể làm thêm các bài tập sau:
Khi giải bài tập về góc, học sinh cần lưu ý những điều sau:
Bài 3.18 trang 37 sách bài tập Toán 8 - Kết nối tri thức với cuộc sống là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng áp dụng kiến thức về các góc tạo bởi đường thẳng cắt đường thẳng. Hy vọng với hướng dẫn chi tiết trên, các em học sinh sẽ hiểu rõ phương pháp giải và tự tin làm bài tập.