Bài 9.67 trang 69 sách bài tập Toán 8 thuộc chương trình Kết nối tri thức với cuộc sống là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng giải bài toán thực tế liên quan đến ứng dụng của tam giác đồng dạng. Bài tập này thường yêu cầu học sinh vận dụng kiến thức về tỉ lệ thức, tam giác đồng dạng để tính toán các độ dài, diện tích trong hình học.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 9.67 trang 69 SBT Toán 8, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Cho tam giác ABC vuông tại A có đường cao AH. Gọi M, N, P lần lượt là trung điểm của HA, HB, HC. Chứng minh rằng:
Đề bài
Cho tam giác ABC vuông tại A có đường cao AH. Gọi M, N, P lần lượt là trung điểm của HA, HB, HC. Chứng minh rằng:
a) $\Delta MNP\backsim \Delta ABC$ và tìm tỉ số đồng dạng
b) $\Delta ABN\backsim \Delta CAM$ và $\Delta ACP\backsim \Delta BAM$
c) \(AN \bot CM\) và \(AP \bot BM\)
Phương pháp giải - Xem chi tiết
a) Sử dụng kiến thức về trường hợp đồng dạng của tam giác để chứng minh tam giác đồng dạng: Trường hợp đồng dạng cạnh – cạnh – cạnh: Nếu ba cạnh của tam giác này tỉ lệ với ba cạnh của tam giác kia thì hai tam giác đó đồng dạng với nhau.
b) Sử dụng kiến thức về trường hợp đồng dạng của tam giác để chứng minh tam giác đồng dạng:
+ Trường hợp đồng dạng cạnh – góc – cạnh: Nếu hai cạnh của tam giác này tỉ lệ với hai cạnh của tam giác kia và góc tạo bởi các cặp cạnh đó bằng nhau thì hai tam giác đó đồng dạng với nhau.
+ Trường hợp đồng dạng góc – góc: Nếu hai góc của tam giác lần lượt bằng hai góc của tam giác kia thì hai tam giác đó đồng dạng với nhau.
c) Sử dụng kiến thức về 3 đường cao trong tam giác: 3 đường cao trong tam giác đồng quy tại một điểm, điểm đó được gọi là trực tâm của tam giác.
Lời giải chi tiết
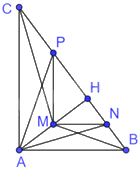
a) Tam giác CAH có P, M lần lượt là trung điểm của CH, AH nên MP là đường trung bình của tam giác ACH, suy ra \(\frac{{MP}}{{AC}} = \frac{1}{2}\)
Tam giác BAH có N, M lần lượt là trung điểm của BH, AH nên MN là đường trung bình của tam giác ABH, suy ra \(\frac{{MN}}{{AB}} = \frac{1}{2}\)
Ta có: \(\frac{{PN}}{{CB}} = \frac{{PH + HN}}{{CH + HB}} = \frac{{PH + HN}}{{2\left( {PH + HN} \right)}} = \frac{1}{2}\)
Tam giác MNP và tam giác ABC có:
\(\frac{{MP}}{{AC}} = \frac{{PN}}{{CB}} = \frac{{MN}}{{AB}} = \frac{1}{2}\) nên $\Delta MNP\backsim \Delta ABC\left( c-c-c \right)$ với tỉ số đồng dạng bằng \(\frac{1}{2}\)
b) Tam giác ABC vuông tại A nên \(\widehat {BAC} = {90^0}\)
Vì AH là đường cao trong tam giác ABC nên \(AH \bot BC\). Do đó, \(\widehat {AHB} = \widehat {AHC} = {90^0}\)
Tam giác ABH và tam giác HAC có:
\(\widehat {AHB} = \widehat {AHC} = {90^0},\widehat {ABH} = \widehat {CAH}\left( { = {{90}^0} - \widehat {ACH}} \right)\)
Do đó, $\Delta HBA\backsim \Delta HAC\left( g-g \right)$. Suy ra: \(\frac{{AB}}{{AC}} = \frac{{BH}}{{AH}} = \frac{{BN}}{{MA}}\)
Tam giác ABN và tam giác CAM có:
\(\widehat {ABN} = \widehat {CAM}\left( {cmt} \right),\frac{{AB}}{{AC}} = \frac{{BN}}{{MA}}\left( {cmt} \right)\)
Do đó, $\Delta ABN\backsim \Delta CAM\left( c-g-c \right)$
Vì $\Delta HBA\backsim \Delta HAC\left( g-g \right)$. Suy ra: \(\frac{{AB}}{{AC}} = \frac{{AH}}{{CH}} = \frac{{AM}}{{CP}}\)
Tam giác ACP và tam giác BAM có:
\(\widehat {ACP} = \widehat {MAB}\left( { = {{90}^0} - \widehat {CAH}} \right),\frac{{AB}}{{AC}} = \frac{{AM}}{{CP}}\left( {cmt} \right)\)
Do đó, $\Delta ACP\backsim \Delta BAM\left( c-g-c \right)$
c) Vì MN là đường trung bình trong tam giác AHB nên MN//AB, mà \(AB \bot AC\) nên \(MN \bot AC\)
Trong tam giác CAN có: \(MN \bot AC\) nên MN là đường cao trong tam giác CAN, AH là đường cao trong tam giác CAN, mà M là giao điểm của MN và AH nên M là trực tâm trong tam giác CAN. Vậy \(CM \bot AN\)
Vì MP là đường trung bình trong tam giác CAH nên MP//AC, mà \(AB \bot AC\) nên \(MP \bot AB\)
Trong tam giác PAB có: \(MP \bot AB\) nên MP là đường cao trong tam giác PAB, AH là đường cao trong tam giác PAB, mà M là giao điểm của MP và AH nên M là trực tâm trong tam giác PAB. Vậy \(AP \bot BM\)
Bài 9.67 trang 69 sách bài tập Toán 8 - Kết nối tri thức là một bài toán ứng dụng thực tế, đòi hỏi học sinh phải hiểu rõ về tam giác đồng dạng và các tính chất liên quan. Dưới đây là hướng dẫn giải chi tiết bài toán này:
Cho hình 39. Biết AB = 6cm, AC = 8cm, AD = 4cm. Tính độ dài AE.
Xét tam giác ABC và tam giác ADE, ta có:
Vậy, tam giác ABC đồng dạng với tam giác ADE (g.g).
Từ sự đồng dạng trên, ta có tỉ lệ thức:
$ rac{AD}{AB} = rac{AE}{AC}$
Thay số vào tỉ lệ thức, ta được:
$ rac{4}{6} = rac{AE}{8}$
Suy ra:
$AE = rac{4 imes 8}{6} = rac{32}{6} = rac{16}{3}$ (cm)
Vậy, độ dài AE là $ rac{16}{3}$ cm.
Bài toán này yêu cầu học sinh vận dụng kiến thức về:
Tam giác đồng dạng: Hiểu rõ các trường hợp đồng dạng của tam giác (g.g, g.g, c.g.c) và các tính chất của tam giác đồng dạng (tỉ lệ các cạnh tương ứng, tỉ lệ các góc tương ứng).
Tỉ lệ thức: Biết cách thiết lập và giải tỉ lệ thức để tìm các đoạn thẳng chưa biết.
Ứng dụng của tam giác đồng dạng: Nhận biết và giải quyết các bài toán thực tế liên quan đến tam giác đồng dạng, ví dụ như tính chiều cao của một vật thể, tính khoảng cách giữa hai điểm.
Để nắm vững kiến thức về tam giác đồng dạng và rèn luyện kỹ năng giải bài tập, các em học sinh có thể tham khảo các bài tập tương tự sau:
Vẽ hình chính xác: Hình vẽ chính xác giúp học sinh dễ dàng nhận biết các yếu tố cần thiết để chứng minh tam giác đồng dạng.
Tìm các góc bằng nhau: Xác định các góc bằng nhau là bước quan trọng để áp dụng các trường hợp đồng dạng của tam giác.
Lập tỉ lệ thức: Sau khi chứng minh tam giác đồng dạng, hãy lập tỉ lệ thức giữa các cạnh tương ứng để tìm các đoạn thẳng chưa biết.
Kiểm tra lại kết quả: Sau khi giải bài tập, hãy kiểm tra lại kết quả để đảm bảo tính chính xác.
Bài 9.67 trang 69 sách bài tập Toán 8 - Kết nối tri thức là một bài tập quan trọng giúp học sinh củng cố kiến thức về tam giác đồng dạng và rèn luyện kỹ năng giải bài toán thực tế. Hy vọng với hướng dẫn chi tiết trên, các em học sinh sẽ tự tin giải bài tập này và đạt kết quả tốt trong môn Toán.