Bài 7.50 trang 37 sách bài tập Toán 8 Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng giải bài toán thực tế liên quan đến các ứng dụng của tam giác đồng dạng. Bài tập này thường yêu cầu học sinh vận dụng kiến thức về tỉ lệ thức, tam giác đồng dạng để giải quyết các vấn đề về chiều cao, khoảng cách.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 7.50 trang 37, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Giả sử rằng lượng cung S và lượng cầu D về áo phông tại một buổi biểu diễn được cho
Đề bài
Giả sử rằng lượng cung S và lượng cầu D về áo phông tại một buổi biểu diễn được cho bởi các hàm số sau: \(S\left( p \right) = - 600 + 10p,D\left( p \right) = 1\,200 - 20p\), trong đó p (nghìn đồng) là giá tiền của một chiếc áo phông.
a) Tìm mức giá cân bằng (tức là mức giá mà lượng cung bằng lượng cầu) của áo phông tại buổi biểu diễn này.
b) Vẽ đồ thị của hai hàm số S(p) và D(p) trên cùng một hệ trục tọa độ.
c) Từ kết quả của câu b, xác định mức giá của áo phông mà lượng cung lớn hơn lượng cầu. Khi đó, điều gì sẽ xảy ra?
Phương pháp giải - Xem chi tiết
a) Để mức giá cân bằng (tức là mức giá mà lượng cung bằng lượng cầu) của áo phông tại buổi biểu diễn này thì \(S\left( p \right) = D\left( p \right)\), từ đó tính được p.
b) Sử dụng kiến thức về cách vẽ đồ thị hàm số bậc nhất \(y = ax + b\left( {a \ne 0} \right)\) để vẽ đồ thị:
+ Khi \(b = 0\) thì \(y = ax\). Đồ thị của hàm số \(y = ax\) là đường thẳng đi qua gốc tọa độ O(0; 0) và điểm A(1; a)
+ Khi \(b \ne 0\), ta thường xác định hai điểm đặc biệt trên đồ thị là giao điểm của đồ thị với hai trục tọa độ như sau:
- Cho \(x = 0\) thì \(y = b\), ta được điểm P(0; b) thuộc trục tung Oy.
- Cho \(y = 0\) thì \(x = \frac{{ - b}}{a}\), ta được điểm \(Q\left( { - \frac{b}{a};0} \right)\) thuộc trục hoành Ox.
- Vẽ đường thẳng đi qua hai điểm P, Q ta được đồ thị của hàm số \(y = ax + b\)
Lời giải chi tiết
a) Theo đầu bài ta có: \(S\left( p \right) = D\left( p \right)\) nên \( - 600 + 10p = 1\;200 - 20p,\)
\(30p = 1\;800\)
\(p = 60\) (nghìn đồng)
b) Đồ thị hàm số \(y = S\left( p \right) = - 600 + 10p\) đi qua \(A\left( {0;\; - 600} \right),G\left( {60;0} \right)\)
Đồ thị hàm số \(y = D\left( p \right) = 1\,200 - 20p\) đi qua \(M\left( {0;\;1\;200} \right),G\left( {60;0} \right)\)
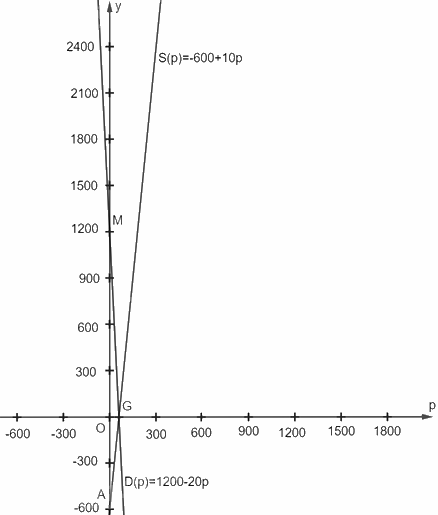
c) Từ đồ thị trên, ta thấy khi giá của mỗi chiếc áo lớn hơn 60 nghìn đồng thì lượng cung lớn hơn lượng cầu. Khi đó, sẽ có một lượng áo phông bị tồn kho vì không bán được.
Bài 7.50 trang 37 sách bài tập Toán 8 Kết nối tri thức yêu cầu học sinh giải quyết một bài toán thực tế liên quan đến việc tính chiều cao của một vật thể dựa trên bóng của nó và góc tạo bởi tia nắng mặt trời. Để giải bài toán này, chúng ta cần hiểu rõ về ứng dụng của tam giác đồng dạng trong việc tính toán các đại lượng liên quan đến hình học.
Một người đứng ở vị trí A cách một cột điện 15m. Người đó đo được góc tạo bởi tia nắng mặt trời và mặt đất là 30°. Biết chiều cao của người đó là 1,6m. Tính chiều cao của cột điện (làm tròn đến chữ số thập phân thứ nhất).
Bài toán này có thể được giải bằng cách sử dụng kiến thức về tam giác đồng dạng. Chúng ta có thể hình dung một tam giác lớn được tạo bởi cột điện, bóng của cột điện và tia nắng mặt trời, và một tam giác nhỏ hơn được tạo bởi người đó, bóng của người đó và tia nắng mặt trời. Hai tam giác này đồng dạng với nhau, do đó chúng ta có thể thiết lập một tỉ lệ thức để tìm chiều cao của cột điện.
Gọi h là chiều cao của cột điện. Ta có:
Vì hai tam giác đồng dạng, ta có tỉ lệ thức:
h / (15 + x) = 1.6 / x
Trong đó x là chiều dài bóng của người đó. Ta có thể tính x bằng công thức:
x = 1.6 / tan(30°)
tan(30°) ≈ 0.577
x ≈ 1.6 / 0.577 ≈ 2.77m
Thay x vào tỉ lệ thức, ta có:
h / (15 + 2.77) = 1.6 / 2.77
h / 17.77 = 0.577
h ≈ 17.77 * 0.577 ≈ 10.24m
Vậy chiều cao của cột điện là khoảng 10.2m.
Để rèn luyện thêm kỹ năng giải bài toán về tam giác đồng dạng, bạn có thể tham khảo các bài tập tương tự trong sách bài tập Toán 8 Kết nối tri thức hoặc trên các trang web học toán online.
Tam giác đồng dạng có rất nhiều ứng dụng trong thực tế, chẳng hạn như:
Giaitoan.edu.vn là một trang web học toán online uy tín, cung cấp đầy đủ các bài giải, lý thuyết và bài tập Toán 8 Kết nối tri thức. Chúng tôi cam kết mang đến cho bạn những trải nghiệm học tập tốt nhất, giúp bạn nắm vững kiến thức và đạt kết quả cao trong môn Toán.