Bài 7.40 trang 33 Sách bài tập Toán 8 - Kết nối tri thức là một bài tập quan trọng trong chương trình học Toán 8. Bài tập này yêu cầu học sinh vận dụng kiến thức đã học về các định lý, tính chất của hình học để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 7.40 trang 33 Sách bài tập Toán 8 - Kết nối tri thức, giúp các em học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
Inch (viết tắt là in) là một đơn vị chiều dài trong hệ đo lường của Mỹ. Phần đường thẳng trong hình vẽ là mô tả sự quy đổi từ x (in) sang y (cm).
Đề bài
Inch (viết tắt là in) là một đơn vị chiều dài trong hệ đo lường của Mỹ. Phần đường thẳng trong hình vẽ là mô tả sự quy đổi từ x (in) sang y (cm).
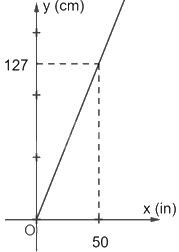
a) Tìm hệ số góc của đường thẳng này.
b) Đại lượng y có tỉ lệ thuận với đại lượng x không? Nếu có thì hệ số tỉ lệ bằng bao nhiêu?
c) Đại lượng y có tỉ lệ thuận với đại lượng x không? Nếu có thì hệ số tỉ lệ bằng bao nhiêu?
Phương pháp giải - Xem chi tiết
a) + Vì đường thẳng đi qua gốc tọa độ (và không trùng với hai trục tọa độ) nên nó là đồ thị của hàm số bậc nhất có dạng \(y = ax\left( {a \ne 0} \right)\)
+ Thay tọa độ điểm (50; 127) vào hàm số ta tìm được a.
+ Sử dụng khái niệm hệ số góc của đường thẳng để tìm hệ số góc của đường thẳng: Ta gọi a là hệ số góc của đường thẳng \(y = ax + b\left( {a \ne 0} \right)\)
b) Sử dụng kiến thức về đại lượng tỉ lệ thuận để xác định xem các đại lượng có tỉ lệ thuận với nhau không và tìm hệ số tỉ lệ: Nếu đại lượng y liên hệ với đại lượng x theo công thức \(y = kx\) (với k là hằng số khác) thì ta nói y tỉ lệ thuận với x theo hằng số tỉ lệ k.
Lời giải chi tiết
a) Vì đường thẳng đi qua gốc tọa độ (và không trùng với hai trục tọa độ) nên nó là đồ thị của hàm số bậc nhất có dạng \(y = ax\left( {a \ne 0} \right)\)
Vì điểm (50; 127) thuộc đồ thị nên \(127 = a.50\), suy ra \(a = \frac{{127}}{{50}} = 2,54\)
Do đó, hệ số góc của đường thẳng là 2,54
b) Vì \(y = 2,54x\) nên đại lượng y tỉ lệ thuận với đại lượng x với hệ số tỉ lệ bằng 2,54
c) Ta có: \(x = \frac{{50}}{{127}}y\) nên đại lượng x cũng tỉ lệ thuận với đại lượng y với hệ số tỉ lệ bằng \(\frac{{50}}{{127}}.\)
Bài 7.40 trang 33 Sách bài tập Toán 8 - Kết nối tri thức thuộc chương trình học Toán 8, tập trung vào việc vận dụng các kiến thức về hình học, đặc biệt là các định lý liên quan đến tam giác đồng dạng và các tính chất của đường thẳng song song. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững lý thuyết và biết cách áp dụng vào thực tế.
Trước khi bắt đầu giải bài tập, điều quan trọng là phải đọc kỹ đề bài và xác định rõ yêu cầu của bài toán. Trong bài 7.40, học sinh cần phân tích hình vẽ, xác định các yếu tố đã cho và tìm ra mối liên hệ giữa chúng. Việc này giúp học sinh có cái nhìn tổng quan về bài toán và lựa chọn phương pháp giải phù hợp.
Để cung cấp lời giải chi tiết, chúng ta cần xem xét cụ thể nội dung của bài toán. Giả sử bài toán yêu cầu chứng minh hai tam giác đồng dạng, học sinh cần chỉ ra các góc bằng nhau hoặc các cạnh tỉ lệ. Sau đó, áp dụng các định lý về tam giác đồng dạng để kết luận.
Ví dụ, nếu đề bài cho tam giác ABC và tam giác A'B'C' có góc A bằng góc A', góc B bằng góc B', thì hai tam giác này đồng dạng theo trường hợp góc - góc (AA). Từ đó, ta có thể suy ra các cạnh tương ứng tỉ lệ nhau.
Các bài toán về tam giác đồng dạng có ứng dụng rộng rãi trong thực tế, như trong kiến trúc, xây dựng, đo đạc,... Ví dụ, để tính chiều cao của một tòa nhà, người ta có thể sử dụng phương pháp tam giác đồng dạng dựa trên bóng đổ của tòa nhà và một vật thể có chiều cao đã biết.
Để nắm vững kiến thức và kỹ năng giải bài tập hình học, học sinh nên luyện tập thêm các bài tập tương tự. Giaitoan.edu.vn cung cấp nhiều bài tập khác với các mức độ khó khác nhau, giúp học sinh rèn luyện và nâng cao khả năng giải toán.
Bài 7.40 trang 33 Sách bài tập Toán 8 - Kết nối tri thức là một bài tập quan trọng giúp học sinh củng cố kiến thức về tam giác đồng dạng và các tính chất của hình học. Bằng cách phân tích đề bài, áp dụng các định lý và tính chất đã học, học sinh có thể giải quyết bài tập một cách hiệu quả. Hãy luyện tập thường xuyên để nâng cao khả năng giải toán và tự tin đối mặt với các bài kiểm tra.