Bài 4.13 trang 52 sách bài tập Toán 8 thuộc chương trình Kết nối tri thức với cuộc sống là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng giải bài toán thực tế liên quan đến các yếu tố hình học và đại số đã học.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 4.13 này, giúp các em học sinh nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Cho \(\Delta ABC\) có AD, BE, CF lần lượt là đường phân giác của góc A, góc B, góc C
Đề bài
Cho \(\Delta ABC\) có AD, BE, CF lần lượt là đường phân giác của góc A, góc B, góc C \(\left( {D \in BC,E \in AC,F \in AB} \right)\). Chứng minh rằng \(\frac{{AE}}{{EC}}.\frac{{CD}}{{DB}}.\frac{{BF}}{{FA}} = 1\).
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức về tính chất đường phân giác của tam giác để chứng minh: Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề với hai đoạn thẳng ấy.
Lời giải chi tiết
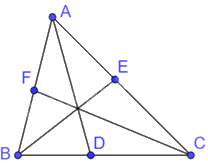
Vì AD là tia phân giác của góc BAC trong tam giác ABC nên \(\frac{{CD}}{{DB}} = \frac{{AC}}{{AB}}\) (tính chất đường phân giác của tam giác)
Vì BE là tia phân giác của góc ABC trong tam giác ABC nên \(\frac{{AE}}{{EC}} = \frac{{AB}}{{BC}}\) (tính chất đường phân giác của tam giác)
Vì CF là tia phân giác của góc BCA trong tam giác ABC nên \(\frac{{BF}}{{FA}} = \frac{{BC}}{{AC}}\) (tính chất đường phân giác của tam giác)
Do đó, \(\frac{{AE}}{{EC}}.\frac{{CD}}{{DB}}.\frac{{BF}}{{FA}} = \frac{{AB}}{{BC}}.\frac{{AC}}{{AB}}.\frac{{BC}}{{AC}} = 1\)
Bài 4.13 trang 52 sách bài tập Toán 8 - Kết nối tri thức với cuộc sống yêu cầu học sinh vận dụng kiến thức về các yếu tố hình học, đặc biệt là các tính chất của hình bình hành, hình chữ nhật, hình thoi và hình vuông, kết hợp với các phép tính đại số để giải quyết các bài toán thực tế.
(Nội dung giải chi tiết bài 4.13 sẽ được trình bày tại đây, bao gồm các bước giải, giải thích rõ ràng và minh họa bằng hình vẽ nếu cần thiết. Bài giải sẽ được chia thành các phần nhỏ để dễ theo dõi và hiểu.)
Ví dụ, bài toán có thể yêu cầu tính diện tích của một hình chữ nhật hoặc hình thoi dựa trên các thông tin về độ dài cạnh hoặc đường chéo. Hoặc bài toán có thể yêu cầu chứng minh một tính chất nào đó của hình học.
Cho hình chữ nhật ABCD có AB = 8cm, BC = 6cm. Tính diện tích hình chữ nhật ABCD.
Giải:
Diện tích hình chữ nhật ABCD là: S = AB.BC = 8cm.6cm = 48cm2
Để củng cố kiến thức và kỹ năng giải bài tập về các yếu tố hình học, các em có thể tự giải các bài tập tương tự sau:
Để học tốt môn Toán 8, các em cần nắm vững lý thuyết, hiểu rõ phương pháp giải bài tập và luyện tập thường xuyên. Hãy dành thời gian ôn tập lại các kiến thức đã học và làm thêm các bài tập để nâng cao kỹ năng giải toán.
Giaitoan.edu.vn hy vọng rằng lời giải chi tiết bài 4.13 trang 52 sách bài tập Toán 8 - Kết nối tri thức với cuộc sống này sẽ giúp các em học sinh học tập tốt hơn. Chúc các em thành công!