Chào mừng các em học sinh đến với bài giải chi tiết bài 1.32 trang 25 SGK Toán 8. Bài học này thuộc chương trình Toán 8, tập trung vào việc vận dụng các kiến thức đã học để giải quyết các bài toán thực tế.
Giaitoan.edu.vn cung cấp lời giải đầy đủ, dễ hiểu, giúp các em nắm vững phương pháp giải và tự tin hơn trong quá trình học tập.
Cho hình thang ABCD có
Đề bài
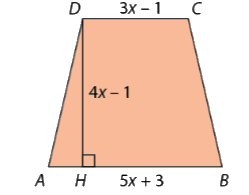
Cho hình thang ABCD có \(AB = 5x + 3,DC = 3x - 1\) và chiều cao \(DH = 4x - 1\) với \(x > 1\) (Hình 1.11). Chứng minh rằng diện tích của hình thang này bằng \(16{x^2} - 1.\)
Phương pháp giải - Xem chi tiết
Sử dụng công thức tính diện tich hình thang, kết hợp với sử dụng 7 hằng đẳng thức đáng nhớ.
Lời giải chi tiết
Diện tích hình thang ABCD là:
\(\frac{{\left( {3x - 1} \right) + \left( {5x + 3} \right)}}{2}\left( {4x - 1} \right) = \frac{{8x + 2}}{2}\left( {4x - 1} \right) = \left( {4x + 1} \right)\left( {4x - 1} \right) = 16{x^2} - 1\)
Vậy diện tích của hình thang này bằng \(16{x^2} - 1.\)
Bài 1.32 trang 25 SGK Toán 8 yêu cầu chúng ta giải một bài toán thực tế liên quan đến việc sử dụng các tính chất của hình bình hành. Để giải bài toán này một cách hiệu quả, chúng ta cần nắm vững các kiến thức cơ bản về hình bình hành, bao gồm:
Nội dung bài toán: (Giả sử bài toán có nội dung cụ thể về một hình bình hành và yêu cầu tính toán các yếu tố liên quan như độ dài cạnh, góc, diện tích,... - Phần này cần được thay thế bằng nội dung bài toán thực tế)
Để giải bài toán này, chúng ta sẽ thực hiện các bước sau:
Ví dụ minh họa: (Giả sử bài toán yêu cầu tính độ dài cạnh của hình bình hành. Chúng ta sẽ sử dụng các tính chất của hình bình hành để thiết lập phương trình và giải phương trình đó để tìm ra độ dài cạnh.)
Lưu ý quan trọng:
Để củng cố kiến thức về hình bình hành, các em có thể làm thêm các bài tập tương tự sau:
Tổng kết:
Bài 1.32 trang 25 SGK Toán 8 là một bài toán quan trọng giúp các em hiểu sâu hơn về hình bình hành và các tính chất của nó. Bằng cách nắm vững các kiến thức cơ bản và áp dụng các phương pháp giải phù hợp, các em có thể giải quyết bài toán này một cách dễ dàng và hiệu quả.
Giaitoan.edu.vn hy vọng rằng bài giải chi tiết này sẽ giúp các em học tập tốt hơn môn Toán 8. Chúc các em thành công!