Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 8. Bài viết này sẽ hướng dẫn bạn giải quyết mục 1 trang 47 SGK Toán 8 một cách nhanh chóng và hiệu quả.
Chúng tôi không chỉ cung cấp đáp án mà còn giải thích rõ ràng từng bước, giúp bạn hiểu sâu sắc kiến thức và rèn luyện kỹ năng giải toán.
Cho phân thức
Cho phân thức \(\frac{{{x^2} - 1}}{{x + 2}}\) và \(\frac{{2 - x}}{x}\) . Hãy nhân tử với tử và mẫu với mẫu của hai phân thức này để được một phân thức mới.
Phương pháp giải:
Sử dụng phép nhân đa thức với đa thức để nhân tử với tử mẫu với mẫu của 2 đa thức này.
Lời giải chi tiết:
\(\left( {{x^2} - 1} \right).\left( {2 - x} \right) = {x^2}\left( {2 - x} \right) - 1\left( {2 - x} \right) = 2{x^2} - {x^3} - 2 + x\)
\(\left( {x + 2} \right).x = {x^2} + 2x\)
Vậy đa thức mới là: \(\frac{{2{x^2} - {x^3} - 2 + x}}{{{x^2} + 2x}}\).
Tính tích của hai phân thức \(\frac{{{x^2} - 4x + 4}}{{y - x}}\) và \(\frac{{{{\left( {x - y} \right)}^2}}}{{3{{\left( {x - 2} \right)}^3}}}\)
Phương pháp giải:
Muốn nhân hai phân thức, ta nhân các tử thức với nhau và các mẫu thức với nhau.
Lời giải chi tiết:
\(\begin{array}{l}\frac{{{x^2} - 4x + 4}}{{y - x}}.\frac{{{{\left( {x - y} \right)}^2}}}{{3{{\left( {x - 2} \right)}^3}}}\\ = \frac{{\left( {{x^2} - 4x + 4} \right).{{\left( {x - y} \right)}^2}}}{{\left( {y - x} \right).3{{\left( {x - 2} \right)}^3}}}\\ = \frac{{{{\left( {x - 2} \right)}^2}.{{\left( {x - y} \right)}^2}}}{{ - \left( {x - y} \right).3{{\left( {x - 2} \right)}^2}}}\\ = \frac{{x - y}}{{ - 3}}\end{array}\)
Tính nhanh: \(\frac{{{x^2} + {y^2}}}{{{x^2}}}.\frac{{{x^2} + 2xy + {y^2}}}{{{{\left( {x - y} \right)}^2}}}.\frac{{{x^2}}}{{{x^2} + {y^2}}}.\frac{{{x^2} - 2xy + {y^2}}}{{{{\left( {x + y} \right)}^2}}}\)
Phương pháp giải:
Sử dụng các hằng đẳng thức đáng nhớ và phương pháp nhân hai phân thức để tính nhanh.
Lời giải chi tiết:
\(\begin{array}{l}\frac{{{x^2} + {y^2}}}{{{x^2}}}.\frac{{{x^2} + 2xy + {y^2}}}{{{{\left( {x - y} \right)}^2}}}.\frac{{{x^2}}}{{{x^2} + {y^2}}}.\frac{{{x^2} - 2xy + {y^2}}}{{{{\left( {x + y} \right)}^2}}}\\ = \frac{{\left( {{x^2} + {y^2}} \right).{{\left( {x + y} \right)}^2}.{x^2}.{{\left( {x - y} \right)}^2}}}{{{x^2}{{\left( {x - y} \right)}^2}.\left( {{x^2} + {y^2}} \right).{{\left( {x + y} \right)}^2}}}\\ = 1\end{array}\)
Tính diện tích của hình chữ nhật trong Hình 2.3 theo x.
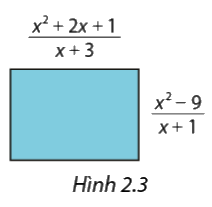
Phương pháp giải:
Áp dụng công thức tính diện tích hình chữ nhật để tính diện tích hình trên theo x.
Lời giải chi tiết:
Diện tích của hình chữ nhật trên là:
\(\begin{array}{l}S = \frac{{{x^2} + 2x + 1}}{{x + 3}}.\frac{{{x^2} - 9}}{{x + 1}} = \frac{{\left( {{x^2} + 2x + 1} \right).\left( {{x^2} - 9} \right)}}{{\left( {x + 3} \right)\left( {x + 1} \right)}} = \frac{{{{\left( {x + 1} \right)}^2}.\left( {x + 3} \right)\left( {x - 3} \right)}}{{\left( {x + 3} \right)\left( {x + 1} \right)}} = \left( {x + 1} \right)\left( {x - 3} \right)\\ = x\left( {x - 3} \right) + 1\left( {x - 3} \right) = {x^2} - 3x + x - 3 = {x^2} - 2x - 3\end{array}\)
Cho phân thức \(\frac{{{x^2} - 1}}{{x + 2}}\) và \(\frac{{2 - x}}{x}\) . Hãy nhân tử với tử và mẫu với mẫu của hai phân thức này để được một phân thức mới.
Phương pháp giải:
Sử dụng phép nhân đa thức với đa thức để nhân tử với tử mẫu với mẫu của 2 đa thức này.
Lời giải chi tiết:
\(\left( {{x^2} - 1} \right).\left( {2 - x} \right) = {x^2}\left( {2 - x} \right) - 1\left( {2 - x} \right) = 2{x^2} - {x^3} - 2 + x\)
\(\left( {x + 2} \right).x = {x^2} + 2x\)
Vậy đa thức mới là: \(\frac{{2{x^2} - {x^3} - 2 + x}}{{{x^2} + 2x}}\).
Tính tích của hai phân thức \(\frac{{{x^2} - 4x + 4}}{{y - x}}\) và \(\frac{{{{\left( {x - y} \right)}^2}}}{{3{{\left( {x - 2} \right)}^3}}}\)
Phương pháp giải:
Muốn nhân hai phân thức, ta nhân các tử thức với nhau và các mẫu thức với nhau.
Lời giải chi tiết:
\(\begin{array}{l}\frac{{{x^2} - 4x + 4}}{{y - x}}.\frac{{{{\left( {x - y} \right)}^2}}}{{3{{\left( {x - 2} \right)}^3}}}\\ = \frac{{\left( {{x^2} - 4x + 4} \right).{{\left( {x - y} \right)}^2}}}{{\left( {y - x} \right).3{{\left( {x - 2} \right)}^3}}}\\ = \frac{{{{\left( {x - 2} \right)}^2}.{{\left( {x - y} \right)}^2}}}{{ - \left( {x - y} \right).3{{\left( {x - 2} \right)}^2}}}\\ = \frac{{x - y}}{{ - 3}}\end{array}\)
Tính diện tích của hình chữ nhật trong Hình 2.3 theo x.
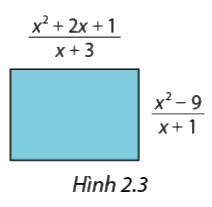
Phương pháp giải:
Áp dụng công thức tính diện tích hình chữ nhật để tính diện tích hình trên theo x.
Lời giải chi tiết:
Diện tích của hình chữ nhật trên là:
\(\begin{array}{l}S = \frac{{{x^2} + 2x + 1}}{{x + 3}}.\frac{{{x^2} - 9}}{{x + 1}} = \frac{{\left( {{x^2} + 2x + 1} \right).\left( {{x^2} - 9} \right)}}{{\left( {x + 3} \right)\left( {x + 1} \right)}} = \frac{{{{\left( {x + 1} \right)}^2}.\left( {x + 3} \right)\left( {x - 3} \right)}}{{\left( {x + 3} \right)\left( {x + 1} \right)}} = \left( {x + 1} \right)\left( {x - 3} \right)\\ = x\left( {x - 3} \right) + 1\left( {x - 3} \right) = {x^2} - 3x + x - 3 = {x^2} - 2x - 3\end{array}\)
Tính nhanh: \(\frac{{{x^2} + {y^2}}}{{{x^2}}}.\frac{{{x^2} + 2xy + {y^2}}}{{{{\left( {x - y} \right)}^2}}}.\frac{{{x^2}}}{{{x^2} + {y^2}}}.\frac{{{x^2} - 2xy + {y^2}}}{{{{\left( {x + y} \right)}^2}}}\)
Phương pháp giải:
Sử dụng các hằng đẳng thức đáng nhớ và phương pháp nhân hai phân thức để tính nhanh.
Lời giải chi tiết:
\(\begin{array}{l}\frac{{{x^2} + {y^2}}}{{{x^2}}}.\frac{{{x^2} + 2xy + {y^2}}}{{{{\left( {x - y} \right)}^2}}}.\frac{{{x^2}}}{{{x^2} + {y^2}}}.\frac{{{x^2} - 2xy + {y^2}}}{{{{\left( {x + y} \right)}^2}}}\\ = \frac{{\left( {{x^2} + {y^2}} \right).{{\left( {x + y} \right)}^2}.{x^2}.{{\left( {x - y} \right)}^2}}}{{{x^2}{{\left( {x - y} \right)}^2}.\left( {{x^2} + {y^2}} \right).{{\left( {x + y} \right)}^2}}}\\ = 1\end{array}\)
Mục 1 trang 47 SGK Toán 8 thường xoay quanh các kiến thức về hình học, cụ thể là các định lý và tính chất liên quan đến tứ giác. Để giải quyết các bài tập trong mục này, học sinh cần nắm vững các khái niệm cơ bản như:
Việc hiểu rõ các khái niệm và định lý này là nền tảng để giải quyết các bài tập một cách chính xác và hiệu quả.
Dưới đây là một số bài tập điển hình thường gặp trong mục 1 trang 47 SGK Toán 8 và hướng dẫn giải chi tiết:
Để chứng minh một tứ giác là hình bình hành, ta có thể sử dụng một trong các cách sau:
Ví dụ: Cho tứ giác ABCD có AB song song CD và AD song song BC. Chứng minh ABCD là hình bình hành.
Giải:
Vì AB song song CD và AD song song BC nên tứ giác ABCD là hình bình hành (dấu hiệu nhận biết hình bình hành).
Trong hình bình hành, các góc đối bằng nhau và các góc kề bù có tổng bằng 180 độ. Để tính các góc của hình bình hành, ta có thể sử dụng các tính chất này.
Ví dụ: Cho hình bình hành ABCD có góc A bằng 60 độ. Tính các góc còn lại.
Giải:
Vì ABCD là hình bình hành nên:
Trong hình thoi, bốn cạnh bằng nhau. Để tính độ dài các cạnh của hình thoi, ta có thể sử dụng định lý Pitago hoặc các tính chất khác của hình thoi.
Ví dụ: Cho hình thoi ABCD có đường chéo AC = 6cm và BD = 8cm. Tính độ dài cạnh của hình thoi.
Giải:
Vì các đường chéo của hình thoi vuông góc với nhau tại trung điểm của mỗi đường nên ta có:
AO = AC/2 = 3cm
BO = BD/2 = 4cm
Áp dụng định lý Pitago vào tam giác vuông AOB, ta có:
AB2 = AO2 + BO2 = 32 + 42 = 25
AB = √25 = 5cm
Vậy độ dài cạnh của hình thoi là 5cm.
Để giải các bài tập về tứ giác một cách nhanh chóng và hiệu quả, bạn có thể áp dụng một số mẹo sau:
Để củng cố kiến thức và rèn luyện kỹ năng giải toán, bạn nên luyện tập thêm các bài tập khác trong SGK Toán 8 và các tài liệu tham khảo khác. Ngoài ra, bạn có thể tham gia các diễn đàn, nhóm học tập trực tuyến để trao đổi kinh nghiệm và học hỏi từ những người khác.
Hy vọng bài viết này đã giúp bạn hiểu rõ hơn về cách giải mục 1 trang 47 SGK Toán 8. Chúc bạn học tập tốt và đạt kết quả cao trong môn Toán!